C - Linear Approximation

概要

長さ $N$ の数列 $A$ が与えられる。ここで関数 $s: \Z \to \Z$ を以下のように定める。

$$ s(b) = \sum_{i=1}^N \left| A_i - (b + i) \right| $$

$s$ の最小値を求めよ。

制約

• $1 \leq N \leq 2 \times 10^5$
• $1 \leq A_i \leq 10^9$

解説

$s(b)$ は $A_i$ の index に依存しているが、上の定義式は書き直すと

$$ s(b) = \sum_{i=1}^N \left| (A_i - i) - b \right| $$

となるため、 $B_i = A_i - i$ なる数列 $B$ を新たに作れば

$$ s(b) = \sum_{i=1}^N \left| B_i - b \right| $$

となり、index に依存しない形になる。これでソートなどの順番を変える操作も行えるようになるので、以降 $B$ は昇順とする。

あとはこの「各要素の $b$ からの距離」の総和を最小化したいわけだが、ここで $B$ の各値を二次元平面にプロットしてみる。横軸を $i$ 、縦軸を $B_i$ とすると、以下のような具合になる。

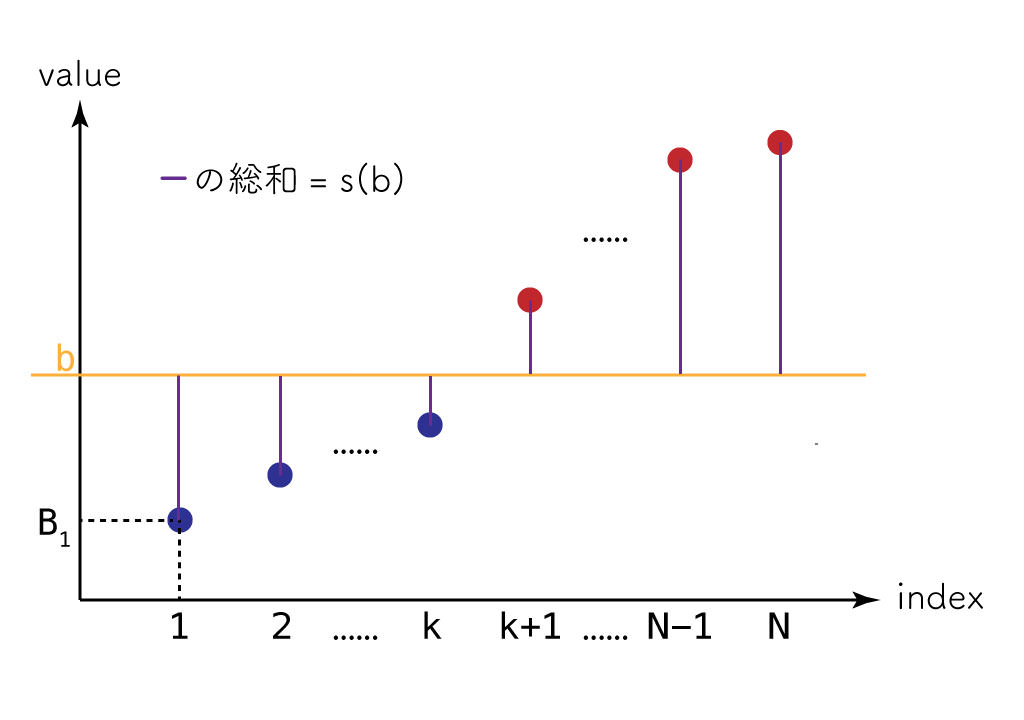
さて、 $b$ が上のように $B_k$ と $B_{k+1}$ の間にあるとき、 $b$ を 1 増やすと $s(b)$ はどれだけ変化するだろうか？

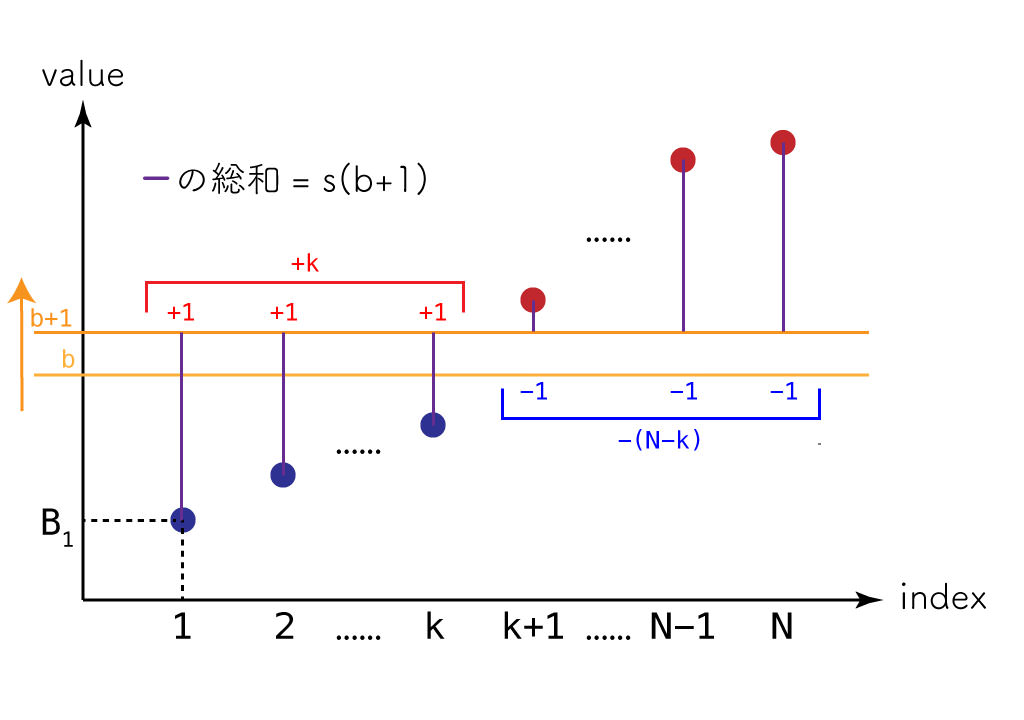
結果は上のように、

• $i \in [1, k]$ については距離が 1 増加
• $i \in [k + 1, N]$ については距離が 1 減少

となるため、 $s(b+1) - s(b) = k - (N - k)$ となる。ここで $d(k) = 2k - N$ としておこう。

$k$ を $\dfrac{N}{2}$ 前後で場合分けすると以下のようになる。

ここから $k \fallingdotseq \dfrac{N}{2}$ で $s(b)$ が最小になることが分かるが、厳密にはどうなるだろうか。これは $N$ が偶数のケースと奇数のケースで場合分けする必要があるが、結果だけ言うとどちらの場合も

$$ b = B_{\frac{N + 1}{2}} $$

として問題ない(小数切り捨て)。0-indexed の場合は b = B[N / 2] となる。 あとはこのときの $s(b)$ を実際に計算すれば AC となる。

計算量はソートがボトルネックとなり $O(N \log N)$ 。中央値を $O(N)$ で出すアルゴリズムもあるらしいが、そこまでする必要はないだろう。

実装例

提出 #3213149 - AtCoder Regular Contest 100

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

#include <algorithm>
#include <iostream>

using namespace std;
using ll = long long;

int main() {
    ll N;
    cin >> N;
    ll A[N];
    for (int i = 0; i < N; ++i) {
        cin >> A[i];
        A[i] -= i + 1;
    }

    sort(A, A + N);
    ll b = A[N / 2];

    ll ans = 0;
    for (int i = 0; i < N; ++i) {
        ans += abs(A[i] - b);
    }

    cout << ans << endl;
    return 0;
}

別解 1: 三分探索

先に上げた表を基準に $s(b)$ のグラフを書いてみると、これは下に凸のグラフになっていることが分かる。 こういった「凸性があるグラフの極値を求めたい」というときに使えるのが、「三分探索」というアルゴリズムである。 ここでは詳しく解説しないが、興味がある方は調べてみるといいだろう。

この解法の計算量は $O(N \log N)$ となる。

別解 2: 累積和

「最適な $b$ は $B_1 \sim B_N$ のどれかだろう」と目星をつければ、累積和を利用することで全探索が可能。具体的には $b = B_k$ の場合

$$ s(B_k) = ((sum_N - sum_k) - (N - k)B_k) + ((k - 1)B_k - sum_{k - 1}) $$

となる。なお $sum_i = B_1 + \dots + B_i$ とする。