AtCoder Regular Contest 099 C

C - Minimization

概要

数列 $(1, 2, \dots , N)$ の順列 $A_i$ がある。この数列に対して以下の操作を何度か行うことで、全ての要素を同じにしたい。

連続する $K$ 個の要素 $A_i, A_{i + 1}, \dots A_{i + K - 1}$ を選ぶ。
これら全てを、その中の最小値で置き換える。

このとき、必要な操作回数の最小値を求めよ。

制約

$2 \leq K \leq N \leq 10^5$

解説

まず数列 $A_i$ が数列 $(1, 2, \dots , N)$ の順列であることから、 全要素の最終的な値が 1 である ことが分かる。なぜなら、最小値である 1 はどのような操作を行っても消すことができないからである。

では実際にどういった操作をすればいいのか。結論を言ってしまうと、操作をした区間全体の集合は、

区間の和は途中で途切れてはならない
区間の和は数列全体を覆っていなくてはならない

という 2 つを満たしていなければならない。

これは、上の操作を「区間全体に最小値を広げる操作」と考えると直感的にもわかりやすいだろう。各条件が満たされていないと、

区間が区切れているところから先に 1 を広げることができない
覆われていない要素に 1 を広げることはできない

ことになり、条件を達成することができない。

逆に、上の 2 条件さえ満たされていれば適用順序を工夫することで必ず全要素を 1 にできる。具体的には、1 が含まれている区間から順番に操作していけばいい。

抽象的すぎて分からないという方は、以下の図が参考になれば幸いである。

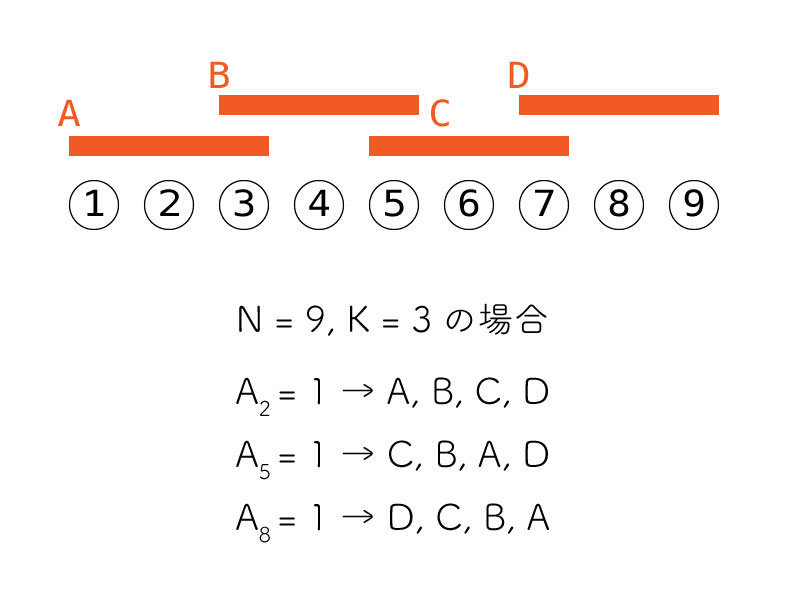
では実際に答えを求めよう。区間数を最小にするためには、区間同士の重なりは 1 にするのが最適である。このとき、 $m$ 個の区間が覆える長さは $(K - 1)m + 1$ となる。これが区間 $[1, N]$ を覆っていればいいわけだから、答えは

$(K - 1)m + 1 \geq N　\Leftrightarrow m \geq \frac{N - 1}{K - 1}$

を満たす最小の $m$ となる。これは、右辺の分数を切り上げることで計算できる。

回答例

提出 #3213090 - AtCoder Regular Contest 099

1
2
3
4
5
6
7
8
9


#include <iostream>
using namespace std;

int main() {
    int N, K;
    cin >> N >> K;
    cout << (N + K - 3) / (K - 1) << endl;
    return 0;
}

$\lceil \frac{a}{b} \rceil = \lfloor \frac{a + b - 1}{b} \rfloor$ で計算できるため、上のような式で答えが求まる。

そして今まで見てきた通り、答えは $N$ と $K$ のみに依存していて 具体的な数列の要素は一切不要 である。こういう場合、上のように標準入力を受け取らずにコードを終了しても問題はない。