AtCoder Regular Contest 074 D

概要

長さ $3N$ の数列 $a$ が与えられる。 $a$ から順番を変えずに $N$ 個の要素を取り除いて、長さ $2N$ の数列 $a'$ を作る。このとき、 $(\text{$a'$ の前半 $N$ 要素の総和})-(\text{$a'$ の後半 $N$ 要素の総和})$ の最大値を求めよ。

制約

$1 \leq N \leq 10^5$
$1 \leq a_i \leq 10^9$

解説

解の求め方

長さ $3N$ の数列から $N$ 要素を消して長さ $2N$ の数列を作り、その前半 $N$ 要素を赤に、後半 $N$ 要素を青に塗ってみる。このとき、元の数列において 赤い要素は全て青い要素より左側にある 。当然といえば当然な性質だが、これがとても重要。

答えとなる塗り分けにおいても、ある一箇所で数列 $a$ を切断することで、その前半には赤い要素だけ、後半には青い要素だけが含まれるようになる。この切断箇所を 1 つ固定する。このとき、 前半は大きい要素から $N$ 個、後半は小さい要素から $N$ 個塗る のが最善となる。

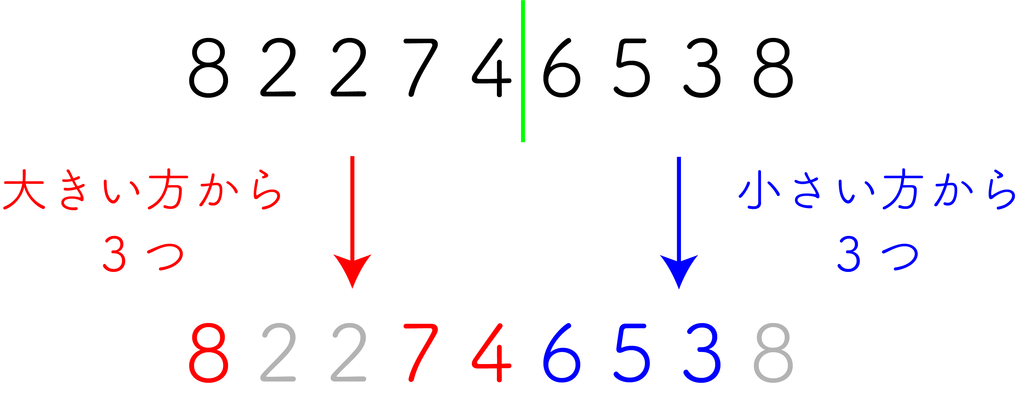
まとめると、全ての切断箇所について前半の上位 $N$ 要素の総和と、後半の下位 $N$ 要素の総和を求めればいい。

計算量の削減

これを高速に求める上で役に立つのが、 優先度付きキュー と呼ばれるデータ構造である。C++では priority_queue という名前が付いている。

これを使えば、以下のようにして赤に塗り分けられた値の総和を順番に調べることができる。

$a_1 \sim a_N$ を priority_queue に突っ込み、その総和を $red_N$ としておく。
以降、以下のようにして $i \in (N, 2N]$ について $red_i$ を求める。
- $red_i = red_{i - 1} + a_i$ とし、 priority_queue に $a_i$ を突っ込む。
- priority_queue から一番小さい要素を取り出し、 $red_i$ から引く。

こうすることで、 priority_queue には常に大きい方から $N$ 個の要素が入っていることになる。青も大小と追加する順番を逆にするだけで同様に実装すればいい。

実装例

提出 #3213388 - AtCoder Regular Contest 074

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73


#include <algorithm>
#include <iostream>
#include <queue>

using namespace std;

using ll = long long;
template <typename T>
using PQ = priority_queue<T>;
template <typename T>
using GPQ = priority_queue<T, vector<T>, greater<T>>;

const ll INF = 1LL << 50;

int main() {
    ll N;
    cin >> N;
    ll a[N * 3 + 1];
    for (int i = 1; i <= N * 3; ++i) {
        cin >> a[i];
    }

    ll red[N * 2 + 1];
    red[0] = 0;
    // red[i] = 前半i個からN個選んだ総和の最大値

    GPQ<ll> rque;
    // 大きい方からN個を保持

    for (int i = 1; i <= N; ++i) {
        red[i] = red[i - 1] + a[i];
        rque.push(a[i]);
    }

    // ここから小さいのが切り捨てられる
    for (int i = N + 1; i <= N * 2; ++i) {
        red[i] = red[i - 1] + a[i];
        rque.push(a[i]);
        red[i] -= rque.top();
        rque.pop();
    }

    // aをひっくり返して同じことをする
    reverse(a + 1, a + N * 3 + 1);

    ll blue[N * 2 + 1];
    blue[0] = 0;
    // blue[i] = 後半i個からN個選んだ総和の最小値

    PQ<ll> bque;
    // 小さい方からN個を保持

    for (int i = 1; i <= N; ++i) {
        blue[i] = blue[i - 1] + a[i];
        bque.push(a[i]);
    }

    for (int i = N + 1; i <= N * 2; ++i) {
        blue[i] = blue[i - 1] + a[i];
        bque.push(a[i]);
        blue[i] -= bque.top();
        bque.pop();
    }

    ll ans = -INF;
    for (int i = N; i <= N * 2; ++i) {
        // 前半i個、後半3N - i個の差
        ans = max(ans, red[i] - blue[N * 3 - i]);
    }

    cout << ans << endl;
    return 0;
}