B - Garbage Collector

概要

数直線上に $N$ 個のゴミとゴミ箱とロボットが置かれている。 ゴミ箱とロボットは座標 0 に、 $i$ 番目のゴミは座標 $x_i$ に置かれている。

これから、ロボットが数直線上を移動してゴミをゴミ箱へ捨てていく。動作にかかるエネルギーは以下の通り。

• ゴミを 1 つ拾うのと、ゴミを 1 回ゴミ箱に入れるのに $X$ 。
  • ゴミをいくつ同時に捨てても、消費するエネルギーは $X$ で変わらない。
• ゴミを $k$ 個持っているとき、1 移動するのに $(k + 1)^2$ 。

また、一度拾ったゴミをゴミ箱以外に置くことはできない。

ロボットが $N$ 個のゴミを全てゴミ箱へ捨てるのに、消費するエネルギーの最小値を求めよ。

制約

• $1 \leq N \leq 2 \times 10^5$
• $0 \lt x_1 \lt \dots \lt x_N \leq 10^9$
• $1 \leq X \leq 10^9$

解説

一度に $K$ 個回収するエネルギー

まず具体例として、「$K$ 個置かれているゴミをまとめてゴミ箱へ捨てる」ときの消費エネルギーを具体的に求める。

まず行動パターンだが、「一番奥まで行って、帰りがけに回収する」というのが最善となる。 これは道中でゴミを拾った場合、一番奥まで行ってそこに戻ってくるまでの間により多くのエネルギーを消費してしまうことから分かる。

では消費エネルギーを計算してみる。以下に $K = 4$ の場合を示す。

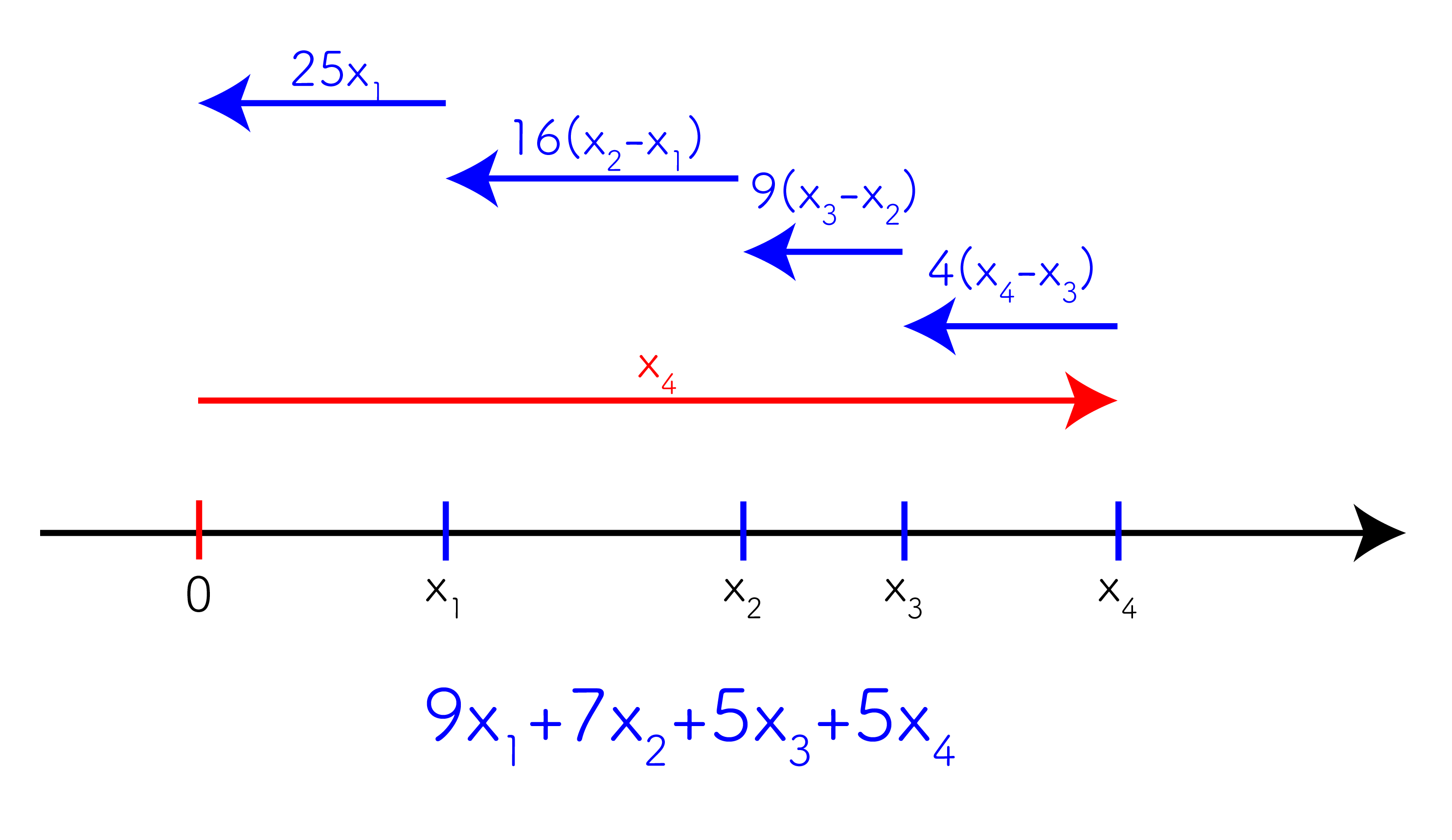
手を動かして計算すると、消費エネルギーは以下のようになる。最後だけ $5$ が連続していることに注意。

$$ (2K + 1)x_1 + (2K - 1)x_2 + \dots + (2K - 2i + 3)x_i + \cdots + 7x_{K - 2} + 5x_{K - 1} + 5x_K $$

往復回数を固定

では、往復回数 $t$ を固定したときのエネルギーの最小値について考えてみよう。 $t = 1$ は上で示した通りなので、次は $t = 2$ について考えてみる。

ただ式で考えると理解しづらいので、「各変数についている係数」を図示して考える。 具体的に $N = 10$ のときを考える。例えばこのとき、1 回目で後ろ 4 個、2 回目で残り 6 個を回収するという方法が考えられる(下図上)。

しかし、回収するゴミを交互にすることで大きい係数を手前にずらすことができるため、そちらの方が効率的である(下図中)。

さらに、回収するゴミの数を 2 回の往復で均一にすることで、全体の係数の最大値をより小さく抑えることができる(下図下)。

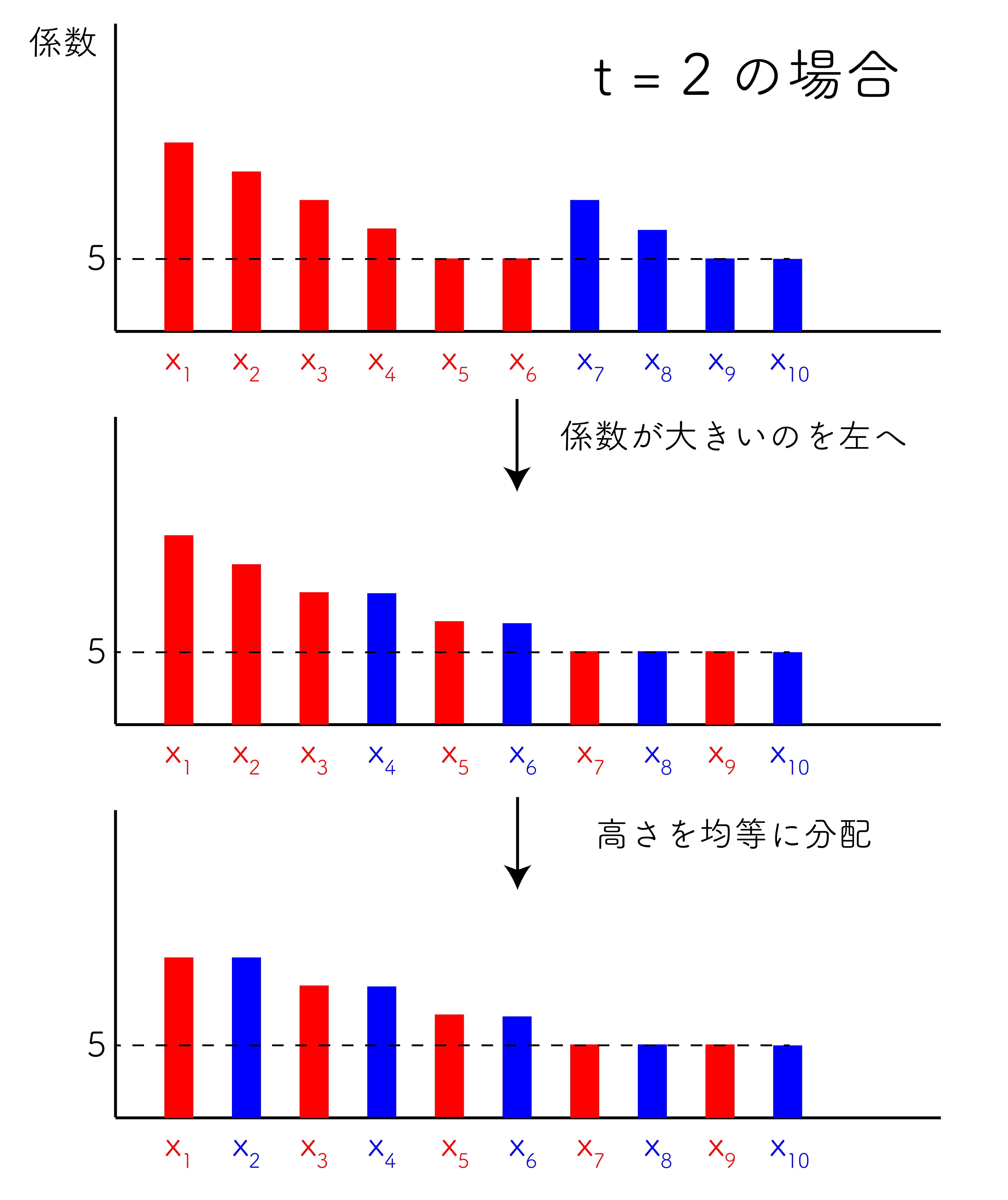
これは $t \gt 2$ でも同じ話で、例えば $t = 3$ なら以下のようになる。

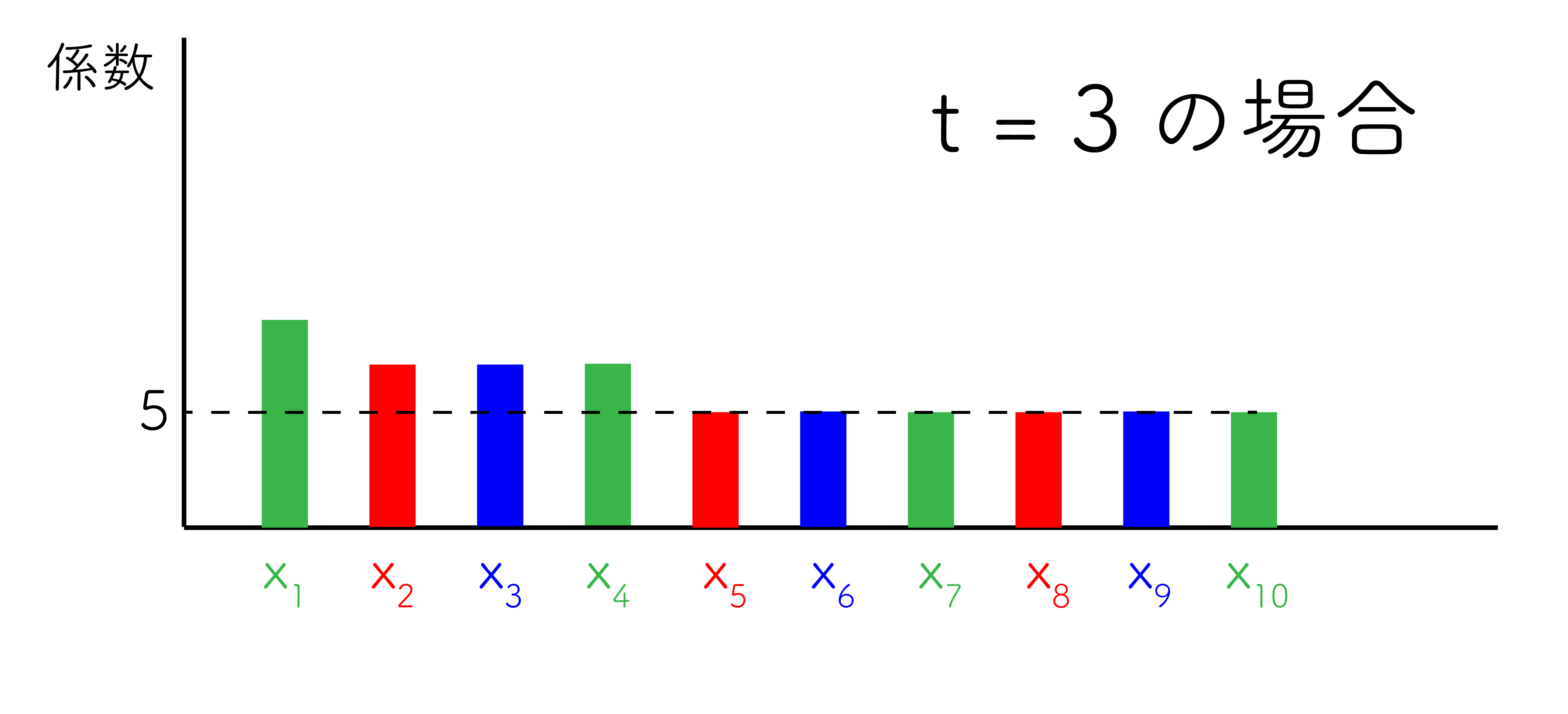
計算量の削減

これで往復回数を固定したときのエネルギーの最小値が分かったが、愚直に計算していると各 $t$ について計算量は $O(N)$ となり部分点しかとれない。

そこで、 $x$ の累積和を予め求めておくことで計算量を削減する。具体的には、右端を $t$ ずつ引きながら累積和を足し上げていけばいい(この辺は言葉で伝えるより下のコードを見た方がわかりやすいと思う)。

一見するとこれでも全体の計算量は $O(N^2)$ から変わらないように見える。しかし、各 $t$ における計算量は正確には $O(N / t)$ であり、調和数列の近似

$$ \frac{1}{1} + \frac{1}{2} + \dots + \frac{1}{N} \simeq \log N $$

から、全体の計算量は $O(N \log N)$ まで落ちていることになる。これで満点が取れる。

実装例

一部の $t$ では 64bit 整数でもオーバーフローを起こす可能性があるため要注意(3 敗)。

提出 #3216762 - AtCoder Grand Contest 027

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

#include <iostream>
using namespace std;
using ll = long long;
const ll INF = 1LL << 60;

int main() {
    ll N, X;
    cin >> N >> X;

    ll sum[N + 1];
    sum[0] = 0;
    for (int i = 1; i <= N; ++i) {
        ll x;
        cin >> x;
        sum[i] = sum[i - 1] + x;
    }

    ll ans = INF;
    for (ll t = 1; t <= N; ++t) {
        // ゴミ捨てとゴミ拾いに消費するエネルギー
        ll cost = (N + t) * X;

        ll now = N;  // 右端

        cost += sum[now] * 5;
        now -= t * 2;
        while (now > 0) {
            cost += sum[now] * 2;
            now -= t;

            // オーバーフロー対策
            if (cost < 0) {
                cost = INF;
                break;
            }
        }
        ans = min(ans, cost);
    }

    cout << ans << endl;
    return 0;
}