D - Worst Case

概要

$10^{10^{10}}$ 人が 2 回のコンテストに参加し、各参加者に独立な順位がつけられた。 コンテストのスコアは、 2 回のコンテストの順位の積によって定義される。

ここで、以下のクエリに $Q$ 回答えよ。

各クエリでは、整数 $A, B$ が与えられる。 このとき、各コンテストで $A$ 位、 $B$ 位をとった高橋くんより、スコアが小さい参加者数の最大値を求めよ。

制約

• $1 \leq Q \leq 100$
• $1 \leq A_i, B_i \leq 10^9$

解説

解の上限

以降、対称性より $A \leq B$ として問題ない。

高橋くんより小さいスコアを取るには、1 回目のコンテストで $A$ 位未満を取るか、2 回目のコンテストで $B$ 位未満を取らなければならない。 よって解の上限は $A + B - 2$ と分かる。

これだけの組数を作るとしたとき、最善なマッチングは以下のようになる。できるだけ大きい値とできるだけ小さい値同士をマッチングさせている。

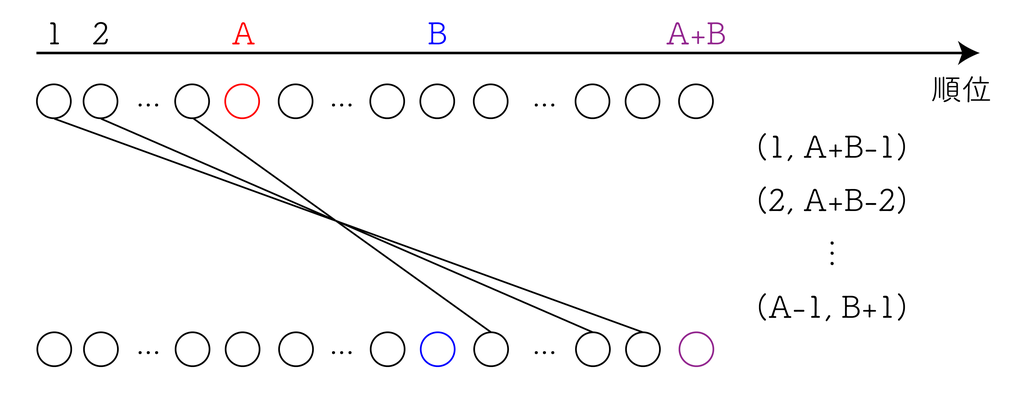
こちらについては、実は $A - 1$ 組全てが条件を満たしている。これは以下の不等式から分かる。

$$ (A - i)(B + i) - AB = (A - B - i)i \lt 0 $$

一方でこちらの $B - 1$ 組は、 $(B, A)$ を含め積が $AB$ 以上となる組が存在するため、このマッチングは成立しない。

解で二分探索

そこで、「後半の組を $K - 1$ 組作ることが可能か？」という問題について考えてみる。 この問題は $K$ について明らかに単調性が成り立つため、二分探索によって最大の $K$ を求めることができる。

そして $K - 1$ 組作る場合の最適なマッチングは、以下のようになる。

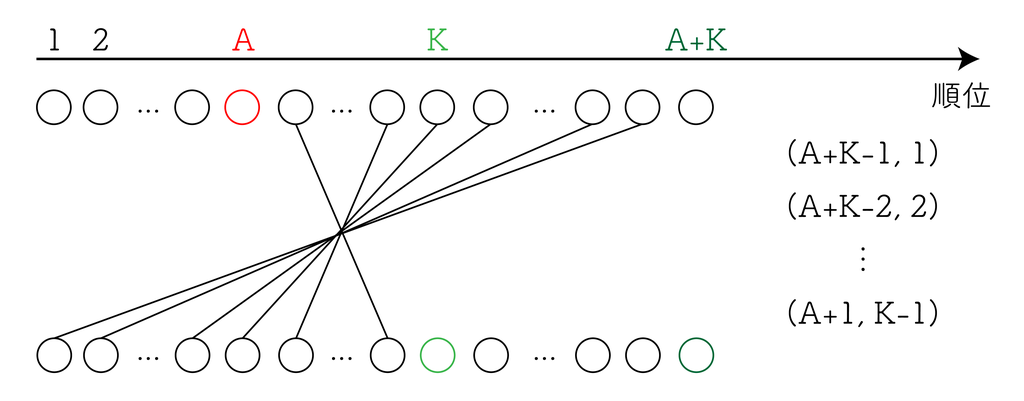
後者の各組は $(A + K - i, K + i)$ と表せるので、 $(A + K + i)(K - i)$ の $0 \leq i \lt K$ における最大値が $AB$ 未満ならこのマッチングは成立することになる。

どの辺で最大値を取るか？

しかし全ての $0 \leq i \lt K$ について を調べていると、当然ながら TLE となる。

では $(A + K + i)(K - i)$ はどの辺で最大値を取るか？ $(a + b)(a - b) = a^2 - b^2$ を考えると、 $b$ が小さい、すなわち $A + K - i \fallingdotseq K - i$ のとき となる。

各組は値の和が $A + K$ であることから、 $m = \lceil (A + K) / 2 \rceil$ とおくと $(m, A + K - m)$ は最も真ん中に近い組となる。 したがって $m (A + K - m)$ が最大値となるため、これと $AB$ の大小を比較すればいい。

ただし $A = K$ の場合のみコーナーケースとなる。 このときは実際に $(A, A)$ の組を取ることがないため、 $m = A - 1$ とする必要がある。そもそも OK の判定にしてしまっても問題ない。

実装例

提出 #3222682 - AtCoder Regular Contest 094

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

#include <iostream>
using namespace std;
typedef long long ll;

int main() {
    int Q;
    cin >> Q;
    for (int q = 0; q < Q; ++q) {
        ll A, B;
        cin >> A >> B;
        if (A > B) {
            swap(A, B);
        }  // A <= B

        ll ok = A, ng = B + 1;
        // K = Aのときは前半と同様にマッチングすればいい

        while (ng - ok > 1) {
            ll K = (ok + ng) / 2;
            ll m = (K + A) / 2;

            // コーナーケース
            if (K == A) --m;

            if (m * (A + K - m) < A * B) {
                ok = K;
            } else {
                ng = K;
            }
        }
        cout << ok + A - 2 << endl;
    }
    return 0;
}