AtCoder Regular Contest 074 C

C - Chocolate Bar

概要

$H \times W$ のグリッド状をした板チョコがある。これを切れ目に沿って長方形に 3 分割したとき、(最大のピースの面積)-(最小のピースの面積)の最小値を求めよ。

制約

$2 \leq H, W \leq 10^5$

解説

いかにも数学っぽい問題だが、数学で解こうとするとパターンが多くて苦戦する。今回は制約が小さいので、プログラムの力でゴリ押すのが吉となる。

まず「最初に横の切れ目で折る」ケースを考える。こうすれば後は、上半分の板チョコをできるだけ 2 等分する問題へ帰着される。2 等分になってしまえば問題は簡単で、ほぼ真ん中の位置で縦と横両方で割ってみればいい。

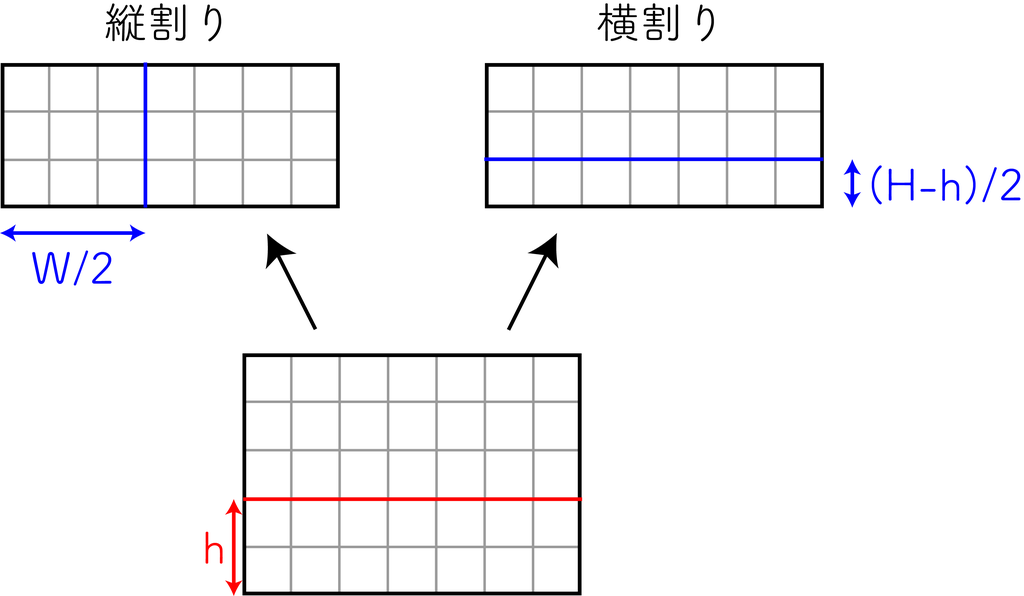
これを全ての切れ目で試せばいい。

残るは「最初に縦の切れ目で折るケース」だが、これはチョコを 90 度回転させれば、先のケースに帰着できる。

実装例

提出 #34748518 - AtCoder Regular Contest 074

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34


#include <algorithm>
#include <iostream>

using namespace std;
using ll = long long;

int main() {
    ll H, W;
    cin >> H >> W;

    ll ans = H * W;
    ll s[3];
    for (int i = 0; i < 2; ++i) {
        for (ll h = 1; h < H; ++h) {
            // まずは縦割り
            s[0] = h * W;
            s[1] = (H - h) * (W / 2);
            s[2] = H * W - (s[0] + s[1]);
            sort(s, s + 3);
            ans = min(ans, s[2] - s[0]);

            // 次いで横割り
            s[0] = h * W;
            s[1] = ((H - h) / 2) * W;
            s[2] = H * W - (s[0] + s[1]);
            sort(s, s + 3);
            ans = min(ans, s[2] - s[0]);
        }
        // 板チョコを90度回す
        swap(H, W);
    }
    cout << ans << endl;
    return 0;
}