B - Mysterious Light

概要

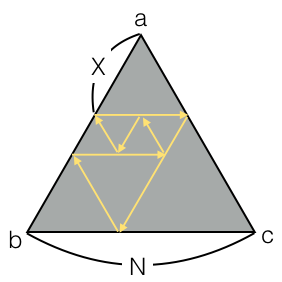
一辺の長さが $N$ の正三角形状に並んだ鏡がある。 この正三角形のある頂点から距離 $X$ の箇所から、他の一辺に対して平行に光線が放たれる。 この光線には特殊な性質があり、鏡だけでなく過去に自分が通った軌道でも反射する。

この光線が放たれてから、再び放たれた点へ戻ってくるまでに通った軌跡の長さを求めよ。

制約

• $2 \leq N \leq 10^{12}$
• $1 \leq X \lt N$

解説

まず、最初に 2 回反射すると下図のようになる。この時点での光路長は $N$ である。

以降は正三角形ではなく、辺の長さが $(X, N - X)$ の平行四辺形について考えることとなる。

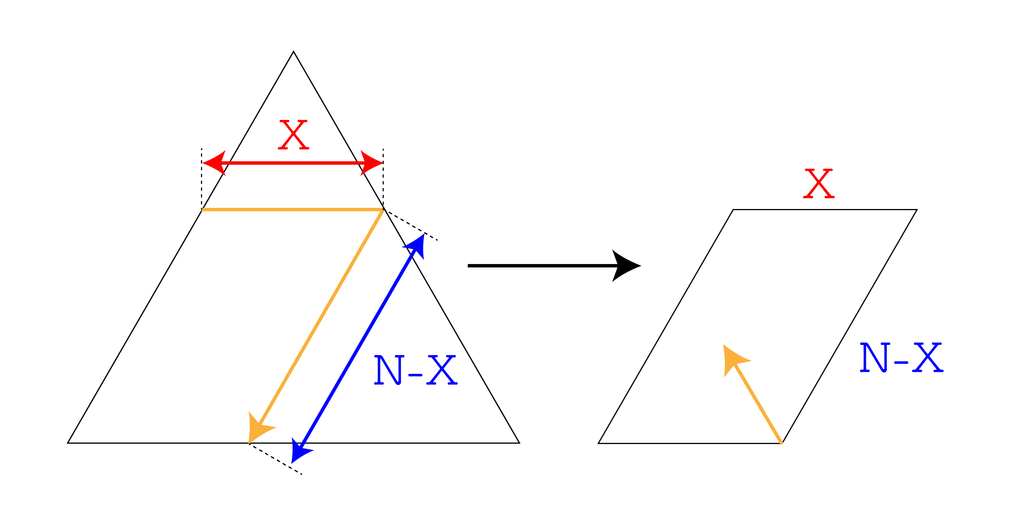
さて、一般化して辺の長さ $(A, B)$ の平行四辺形について考えよう。ただし $A \lt B$ とする。 このとき、 $B$ が $A$ の倍数か否かで場合分けする。

$B$ が $A$ の倍数でない場合

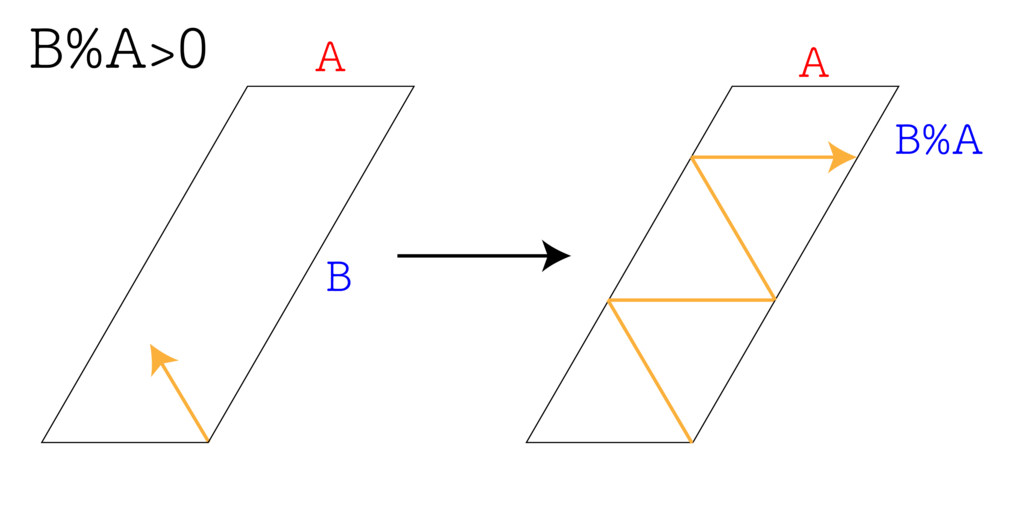
このときの光の軌跡は以下の通り。右の壁に跳ね返る回数は $\lfloor \frac{B}{A} \rfloor$ 回なので、光路長は $A \cdot 2 \lfloor \frac{B}{A} \rfloor$ となる。

そして新たに $(B \bmod A, A)$ の平行四辺形が出現するので、これについて再帰的に調べることになる。

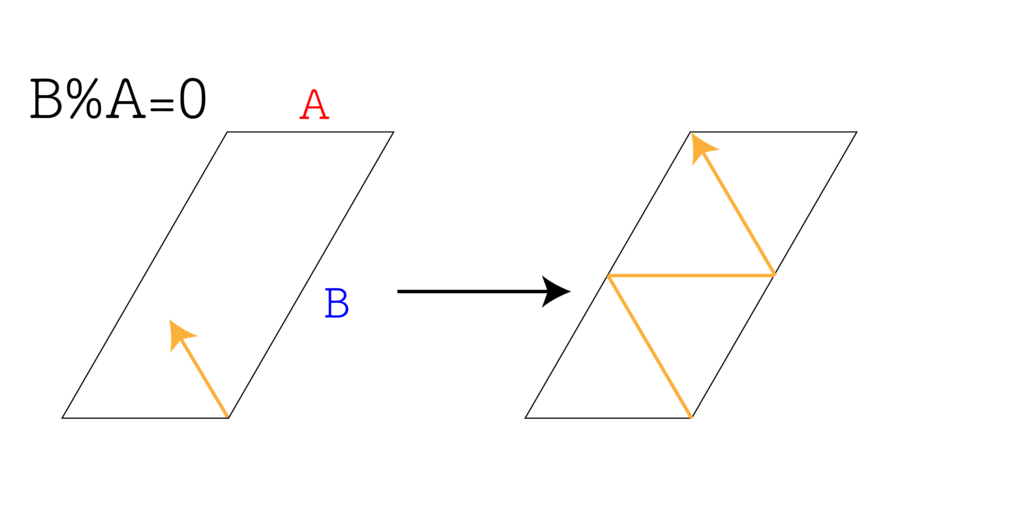
$B$ が $A$ の倍数である場合

このときの光の軌道は以下の通りで、光は出発点に帰ってくる。 光路長は先の場合より短くなって、 $A \times (2 \cdot \frac{B}{A} - 1) = 2B - A$ となる。

以上を再帰関数を使って実装すればいい。

実装例

提出 #3218003 - AtCoder Grand Contest 001

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

#include <iostream>
using namespace std;
using ll = long long;

// (A, B)の平行四辺形内での軌道の長さ
ll reflect(ll A, ll B) {
    if (A > B) swap(A, B);

    ll ref = B / A;
    if (B % A == 0) {
        return (ref * 2 - 1) * A;
    } else {
        return ref * 2 * A + reflect(B % A, A);
    }
}

int main() {
    ll N, X;
    cin >> N >> X;
    cout << N + reflect(X, N - X) << endl;
    return 0;
}