概要
正の整数 $n$ に対して、$S_n$ を以下のように定める: $$ S_n = \sum_{x = 1}^{n} \sum_{y = 1}^{n} \sum_{z = 1}^{n} \left\lfloor \frac{n}{\lcm(x, y, z)} \right\rfloor $$
$S_n$ が奇数となるような、$1$ 以上 $2^{20}$ 未満の $n$ の個数を求めよ。
解説
x, y, z の対称性
$x, y, z$ が全て相異なる場合を考える。このとき $x, y, z$ の順番を変えても $\lcm(x, y, z)$ の値は変わらない。そして $x, y, z$ の並び替え方は 6 通りあるので、$\left\lfloor\frac{n}{\lcm(x, y, z)}\right\rfloor$ は $S_n$ に計 6 回足される。したがって $\left\lfloor\frac{n}{\lcm(x, y, z)}\right\rfloor$ が偶数だろうが奇数だろうが、$S_n$ の偶奇には影響しない。
同様に $x, y, z$ が 2 種類の整数からなる場合を考える。それらを $a, b$ とすると、$(a, a, b)$ の並び替えが 3 通り、$(a, b, b)$ の並び替えも 3 通りなので、$\left\lfloor\frac{n}{\lcm(a, b)}\right\rfloor$ は $S_n$ に計 6 回足される。よって先と同様に、この場合も $S_n$ の偶奇には影響しない。
以上より、$x = y = z$ のケースのみが $S_n$ の偶奇に寄与する。すなわち以下が成り立つ:
$$ S_n \equiv \sum_{x = 1}^{n} \left\lfloor \frac{n}{x} \right\rfloor \pmod{2} $$
格子点の対称性
次は $\sum_{x = 1}^{n} \left\lfloor \frac{n}{x} \right\rfloor$ の偶奇が知りたい。
ここでグラフを描いてみる。以下は $n = 12$ のケースで、上の式の値は格子点の数と一致する:
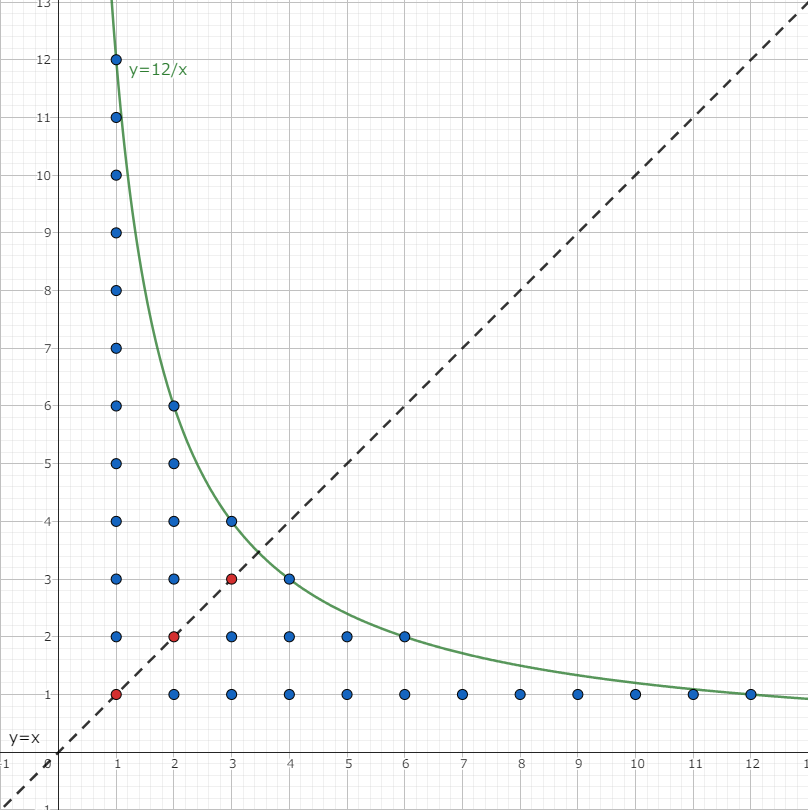
すると、格子点が点線 $y = x$ について対称に配置されていることが分かる。 $y = x$ 上にない青い格子点は、対称な位置にある格子点とペアにできるので、$y = x$ 上にある赤い格子点の個数が、全体の偶奇を決めている。赤い格子点は $\lfloor \sqrt{n} \rfloor$ 個なので、以下が成り立つ:
$$ S_n \equiv \left\lfloor \sqrt{n} \right\rfloor \pmod{2} $$
数え上げ
後は、$\sqrt{n}$ が奇数であるような $n$ を数え上げればいい。
非負整数 $k$ について、$\left\lfloor \sqrt{n} \right\rfloor = 2k + 1$ を満たす $n$ は半開区間 $[(2k + 1)^2, (2k + 2)^2)$ に入っている。 今回は $1 \leq n \lt 2^{20}$ の範囲を数えるので、$1 \leq (2k + 1)^2$ かつ $(2k + 2)^2 \leq 2^{20}$、すなわち $0 \leq k \leq 2^{9} - 1$ の範囲で数えればいい。よって答えは以下のように求まる:
$$ \begin{aligned} \sum_{k = 0}^{2^9 - 1} \left( (2k + 2)^2 - (2k + 1)^2 \right) &= \sum_{k = 0}^{2^9 - 1} (4k + 3) \\ &= 4 \cdot \frac{1}{2} \cdot (2^9 - 1) \cdot 2^9 + 3 \cdot 2^9 \\ &= 2^9 (2^{10} + 1) \\ &= \underline{524800} \end{aligned} $$