概要
正方形 $ABCD$ があり、$\triangle ADC$ 内部の点 $P$ と、$\triangle ABC$ 内部の点 $Q$ が以下を満たしている:
- $\angle APQ = \angle PQC = 90 \degree$
- $AP = 10, PQ = 8, BQ = 9$
なお、この条件を満たす図形は一意に存在する。
線分 $CQ$ の長さを求めよ。
解説
問題文の条件を全て満たすように、座標平面上に点 $A, P, Q$ を以下のように配置する:
$$ A = (-10, 8), \; P = (0, 8), \; Q = O = (0, 0) $$
すると $\angle PQC = 90 \degree$ より、点 $C$ は x 軸上に来る。
$BQ = 9$ より、パラメータ $\theta$ を用いて $B = (9 \cos \theta, 9 \sin \theta)$ と表せる。 そして $\overrightarrow{BC}$ は $\overrightarrow{BA}$ を時計回りに $90 \degree$ 回転させたものなので1、点 $C$ の座標は以下のように求まる:
$$ \begin{aligned} \overrightarrow{BA} &= (-10 - 9 \cos \theta, 8 - 9 \sin \theta) \\ \overrightarrow{BC} &= (8 - 9 \sin \theta, 10 + 9 \cos \theta) \\ \overrightarrow{OC} &= \overrightarrow{OB} + \overrightarrow{BC} \\ &= (8 + 9 (\cos \theta - \sin \theta), 10 + 9 (\cos \theta + \sin \theta)) \\ &= \left( 8 + 9 \sqrt{2} \cos \left( \theta + \frac{\pi}{4} \right), 10 + 9 \sqrt{2} \cos \left( \theta - \frac{\pi}{4}\right) \right) \\ \end{aligned} $$
そして点 $C$ は x 軸上にあるので、その y 座標は 0 でなければならない。よって、以下のように点 $C$ の座標が求まる:
$$ \begin{aligned} 10 + 9 \sqrt{2} \cos \left( \theta - \frac{\pi}{4}\right) &= 0 \\ \cos \left(\theta - \frac{\pi}{4}\right) &= - \frac{10}{9 \sqrt{2}} = - \frac{5 \sqrt{2}}{9} \\ \sin \left(\theta - \frac{\pi}{4}\right) &= \pm \sqrt{1 - \cos^2 \left(\theta - \frac{\pi}{4}\right)} = \pm \frac{\sqrt{31}}{9} \\ \cos \left(\theta + \frac{\pi}{4}\right) &= - \sin \left(\theta - \frac{\pi}{4}\right) = \pm \frac{\sqrt{31}}{9} \\ 8 + 9 \sqrt{2} \cos \left( \theta + \frac{\pi}{4} \right) &= 8 \pm 9 \sqrt{2} \cdot \frac{\sqrt{31}}{9} = 8 \pm \sqrt{62} \end{aligned} $$
このように 2 つ解が出るのだが2、図にするとそれぞれ以下のようになる (前者が正の場合、後者が負の場合):

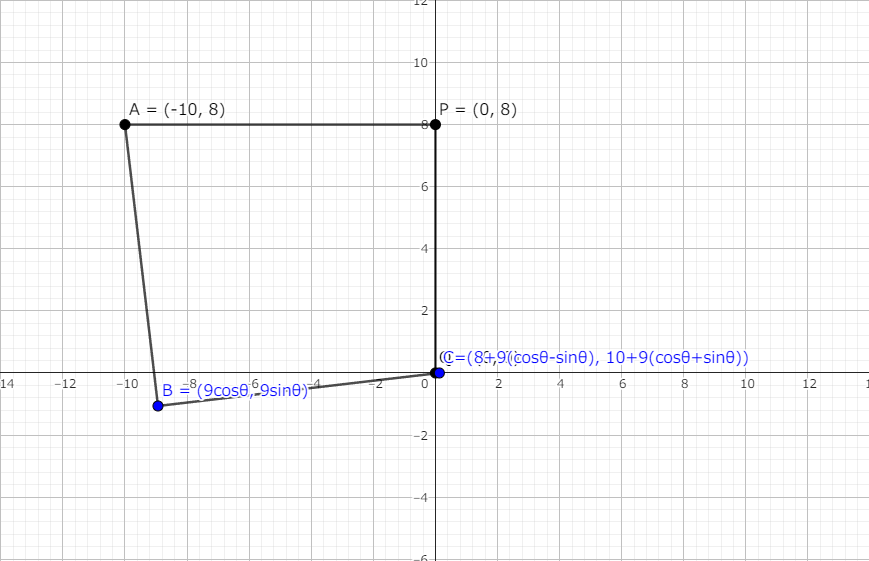
このうち後者は、点 $P$ が $\triangle ACD$ の外に出てしまうため不適。
したがって点 $C$ の x 座標、すなわち $\underline{QC = 8 + \sqrt{62}}$。