2631 < JAG Summer < Challenges | Aizu Online Judge
問題
長さ $n$ の整数列 $(a_i)$ が与えられる。以下を満たすような頂点の選び方が存在する、最小の $m$ を求めよ。
- $m$ 頂点完全グラフがある。最初全ての辺に色はついていない。
- 各 $i$ に対して $a_i$ 個の頂点を選び、それらの間に張られている辺を全て色 $i$ で塗る。
- 最終的に 2 色以上で塗られた辺は存在しなかった。
制約
- $1 \leq n \leq 5$
- $2 \leq a_i \leq 10^9$
考察
各 $i$ について、選ばれた頂点集合を $U_i$ とする ($|U_i| = a_i$)。
すると「最終的に 2 色以上で塗られた辺は存在しなかった」という条件は、「任意の $i \neq j$ について、 $|U_i \cap U_j| \lt 2$ 」と同値となる。
一方で $m$ を最小化するためには、 $(U_i)$ はできるだけ互いに多くの共通部分を持っている方がよい。
以降 $(a_i)$ は降順に並んでいるものとする。ここで $a_1 \geq n - 1$ の場合、以下のように $U_1$ と他の集合がそれぞれ相異なる 1 点で交わるようにするのが最善となる。

このように配置した場合、残りは各 $a_i$ が 1 ずつ減ったケースに帰着される( $a_i = 0$ なら消す)ので、帰納的に解くことができる。
そうでない場合、 $m$ の小さい方から $U_i$ の選び方を全探索する。最大ケースは $(3, 3, 3, 3, 3)$ だが、これは以下のように $m = 7$ で達成できる。
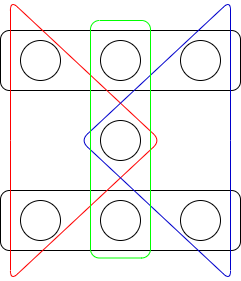
つまり全探索は $m \leq 7$ で止まる。そして以下の式から分かるように、計算量もそこまで大きくならない。
$$
\prod_{i=1}^{n} \binom{m}{a_i} \leq \binom{7}{3}^5 \leq 5.3 \cdot 10^7
$$
実装例
Run #4816018 < misteer < Solutions | Aizu Online Judge
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
|
#include <iostream>
#include <algorithm>
#include <vector>
using lint = long long;
void solve() {
int n;
std::cin >> n;
std::vector<lint> xs(n);
for (auto& x : xs) std::cin >> x;
std::sort(xs.rbegin(), xs.rend());
lint ans = 0;
auto abort = [&]() {
std::cout << ans << "\n";
std::exit(0);
};
while (n > 0) {
// xs[0] >= n - 1なら1つ下へ帰着
auto f = xs.front();
if (f < n - 1) break;
ans += f;
xs.erase(xs.begin());
for (auto& x : xs) --x;
while (!xs.empty() && xs.back() == 0) xs.pop_back();
n = xs.size();
}
if (n == 0) abort();
int m;
std::vector<int> ys(n);
auto dfs = [&](auto&& f, int i) -> void {
if (i == n) abort();
auto& y = ys[i];
for (y = 0; y < (1 << m); ++y) {
if (__builtin_popcount(y) != xs[i]) continue;
bool flag = true;
for (int j = 0; j < i; ++j) {
if (__builtin_popcount(ys[j] & y) > 1) flag = false;
}
if (flag) f(f, i + 1);
}
};
for (m = 1;; ++m) {
++ans;
dfs(dfs, 0);
}
}
|

