D - All Your Paths are Different Lengths
概要
整数 $L$ が与えられる。以下を全て満たす有向グラフを 1 つ構築せよ。
- 頂点は $20$ 個以下。
- 辺は $60$ 本以下。
- 各辺の長さは $0$ 以上 $10^6$ 以下の整数。
- 辺は全て番号の小さい頂点から大きい頂点へと張られている。
- 頂点 $1$ から頂点 $N$ へのパスはちょうど $L$ 個あり、それらの長さは $0$ 以上 $L - 1$ の相異なる整数。
制約
解説
こういう「$0 \sim X$ までの整数を全部作れ」という問題は、「$p$ 進法を使う」と上手くいくことが多い。
この問題では、 $p = 2$ で構成できる。
大まかに引く
頂点は常に $20$ 個とする。そして、以下のように辺を張る。
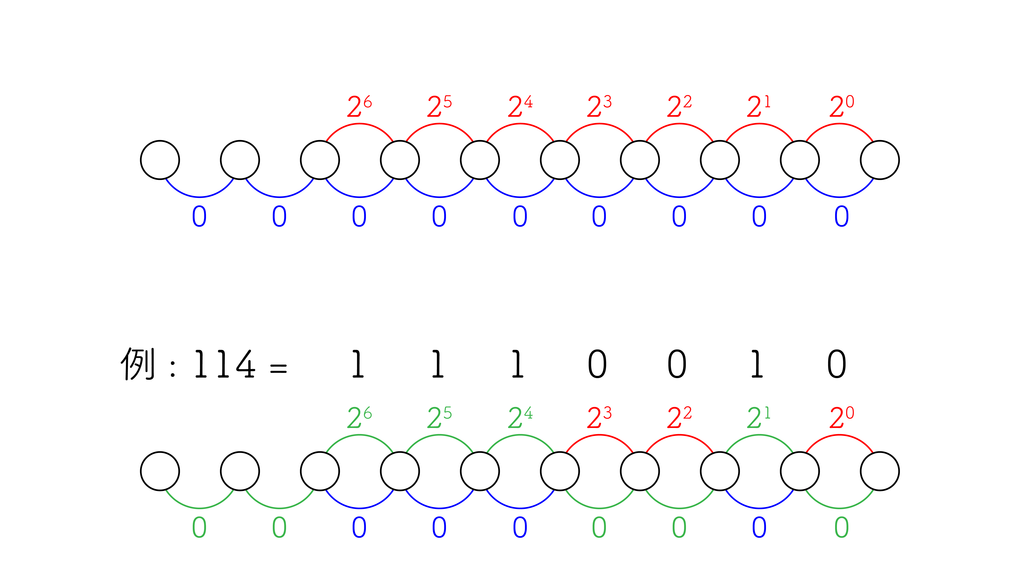
これで $K$ 本の辺を張ったとき、 $[0, 2^K)$ の任意の整数を作ることができる。
辺を張れる数は最大 $19$ 本なので、 $2^{19} - 1 = 524,287$ まで作ることができる。
バイパスで調整
具体例として、 $L = 334$ で考えてみる。
上のように $8$ 本の辺を張ることで、 $[0, 256)$ までは作れる。
しかし $9$ 本張ってしまうと $[0, 512)$ まで作れてしまい、パスが多すぎとなる。
ではどうやって $[256, 334)$ を作るか?
そこで $256$ を後から加えることにして、 $[0, 78)$ を作ることを考える。
これは上と同様の方法で 6 本の辺によって $[0, 64)$ までなら作れる。
ということで、6 本の辺の先、つまり頂点 7 から 20 に向けて長さ $256$ の バイパス を張ることで $[256, 320)$ のパスが新たに増える。
残りは $[320, 334)$ なので、次は $320$ を引いて $[0, 14)$ を作って……と考えることで、最終的に $[0, 334)$ のパスが全部できる。
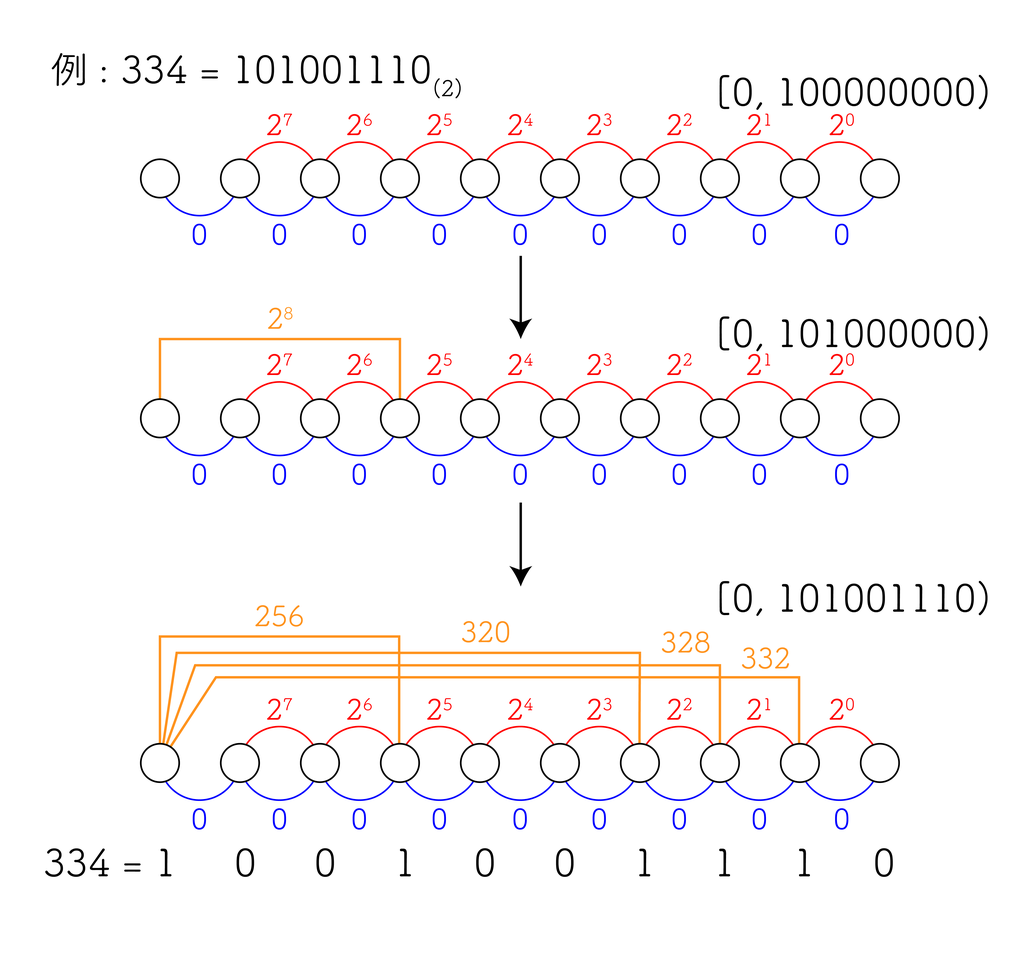
ちなみに一番下にあるように、バイパスの始点は $L$ の bit と一致している。
実装例
提出 #3230608 - AtCoder Regular Contest 102
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
|
#include <iostream>
#include <vector>
using namespace std;
using ll = long long;
struct edge {
int from;
int to;
int cost;
edge(int _from, int _to, int _cost) : from(_from), to(_to), cost(_cost){};
};
vector<edge> ans;
// [add, add + L)のバイパスを作る
void bypass(int add, int L) {
if (L <= 0) return;
for (int k = 19; k >= 0; --k) {
if (L >= (1 << k)) {
// [add, add + 2^k)を作る
// k本の辺の後、つまり頂点k+1から20に辺を張る
ans.push_back(edge(k + 1, 20, add));
// [add + 2^k, add + L)を作る
bypass(add + (1 << k), L - (1 << k));
break;
}
}
return;
}
int main() {
int L;
cin >> L;
// 0の辺を全部張る
for (int i = 1; i < 20; ++i) {
ans.push_back(edge(i, i + 1, 0));
}
// 大まかにグラフを作る
for (int k = 19; k >= 1; --k) {
if (L >= (1 << k)) {
// k本辺を張って[0, 2^k)を作る
for (int i = 1; i <= k; ++i) {
ans.push_back(edge(i, i + 1, 1 << (i - 1)));
}
// [2^k, L)を作る
bypass(1 << k, L - (1 << k));
break;
}
}
cout << 20 << " " << ans.size() << endl;
for (auto e : ans) {
cout << e.from << " " << e.to << " " << e.cost << endl;
}
return 0;
}
|

