概要
数列 $(1, 2, \dots, N)$ の順列 $a$ が与えられる。以下の値を求めよ。
$$ \sum_{l = 1}^{N} \sum_{r = l}^{N} \min(a_l, a_{l+1}, \dots, a_r) $$
制約
- $1 \leq N \leq 2 \times 10^5$
解説
全区間に対して最小値を求めようとすると、そもそも区間が $O(N^2)$ 個あるので全く間に合わない。 ここで発想の転換が必要となる。「各区間の最小値はいくつか?」の代わりに「最小値が $i$ になる区間はいくつあるか?」を求めることでも、この問題は解くことができる。このテクニックは俗に「主客転倒」と呼ばれる。
そして最小値が $i$ になる区間の個数は、左右両方について「一番近くにある $i$ より小さい要素」の位置が分かれば、以下のように求められる。
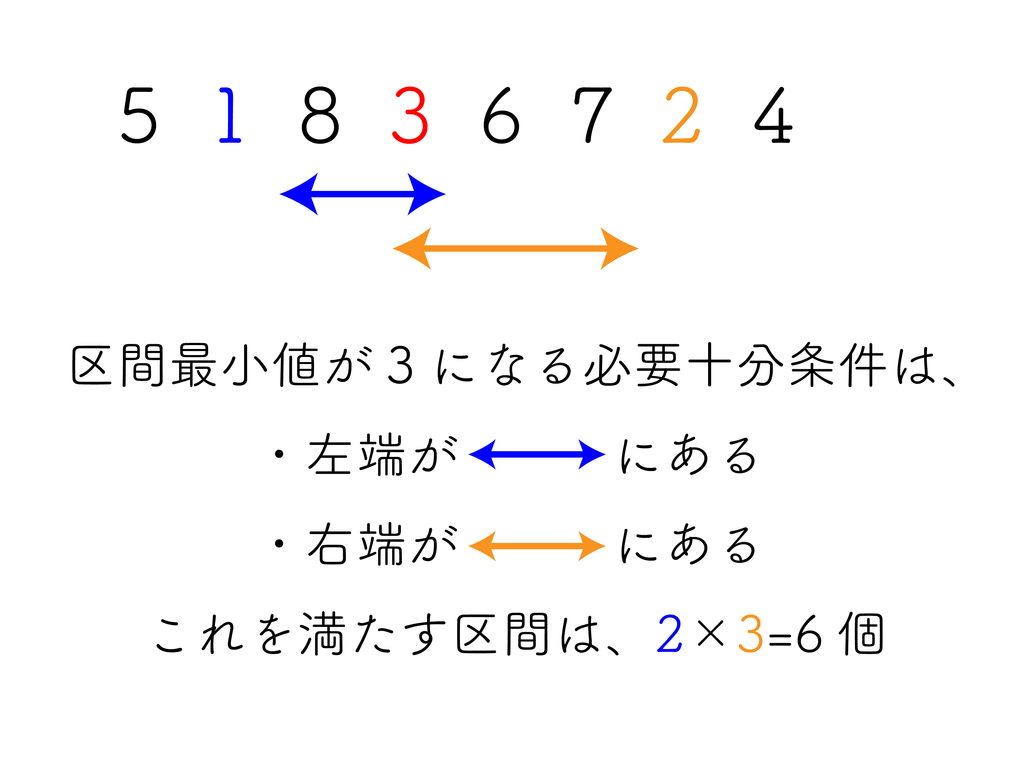
「自分より小さい要素」にしか興味がないので、 小さい値から順に数列に加えていく ことを考える。 こうすると、「既に数列に存在している値は、全て今見ている値より小さい」という性質が成り立って都合がいい。 これにより、「既に加えられた要素のうち、一番近くにあるものの位置」を求める、という問題に言い換えられた。
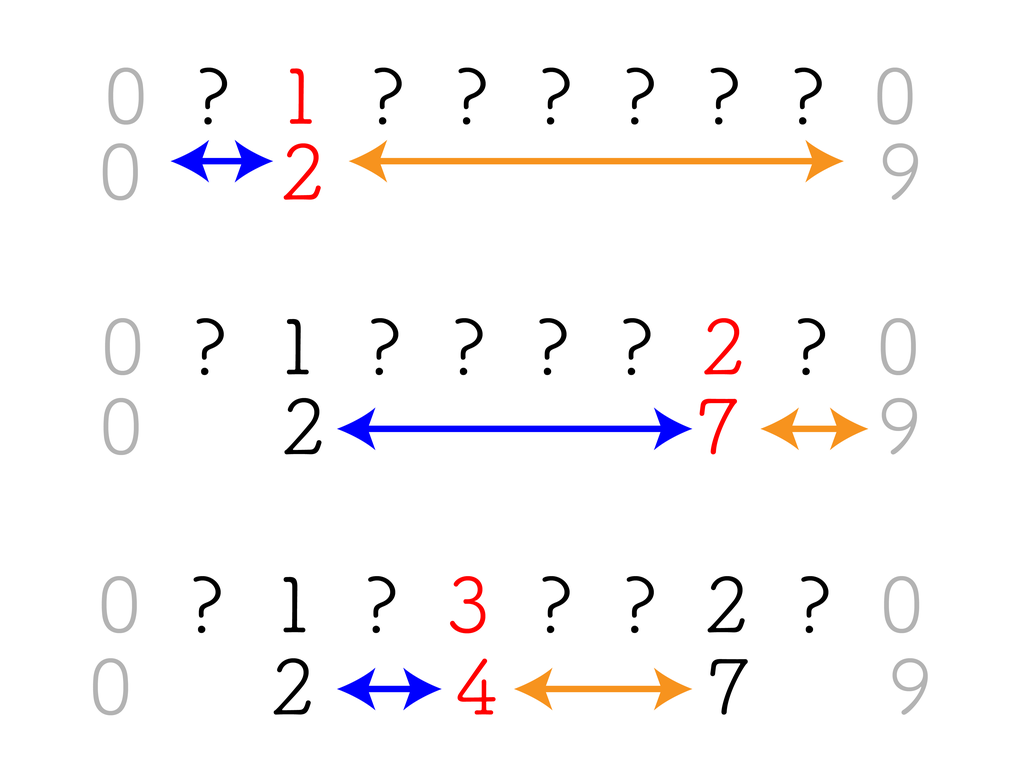
後は実装だが、例えば std::set(平衡二分探索木) の lower_bound(x) を使えば、既に追加された要素のうち x 以上で最小のものを $O(\log N)$ で求められる。この場合、全体の計算量は $O(N \log N)$ となる。
実装例
提出 #3281109 - AtCoder Grand Contest 005
|
|