D - Number of Amidakuji
本記事では、この問題を想定解である $O(H W 2^W)$ 時間より遥かに速い、 $O(W^3 \log H)$ 時間で解く方法を解説する。
問題
鉛直な縦棒 $W$ 本からなるあみだくじについて考える。
各縦棒の長さは $H+1$ であり、端点からの距離が正整数の場所にのみ水平な横棒を引くことができる。つまり、各縦棒からは最大 $H$ 本の横棒を引くことができる。
ただし各横棒は隣接していてはならず、また隣り合う 2 本の縦棒の間にしか引くことはできない。
一番左の縦棒から始めると、最終的に左から $K$ 本目の縦棒に行き着くようなあみだくじの個数を求めよ。
制約
- $1 \leq H \leq 100$
- $1 \leq W \leq 8$
- $1 \leq K \leq W$
解説
$dp_{i, j} =$ 「$i$ 段からなり、1 が $j$ に移動するようなあみだくじの総数」とする。
またこれ以降、一次元配列 $dp_i$ を線型代数における「ベクトル」とみなすことがしばしばある。
あみだくじと行列
まず、あみだくじの形状というのは「置換行列」という線形代数の概念で表現できる。
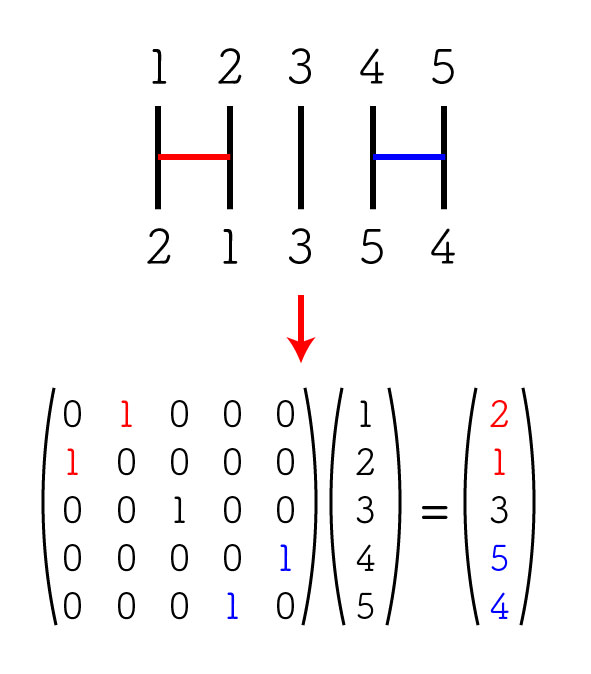
こんな具合に、「基本行列の、横線が入る場所だけ列が入れ替わったもの」があみだくじを表現する行列となる。
したがって、全ての 1 段からなるあみだくじについてこの行列を求め、それぞれベクトル $dp_i$ に掛けて、それらを足し合わせれば $dp_{i + 1}$ が求まる。
さらに行列積の線型性から、これらの行列を全て足し合わせてから $dp_i$ に掛けても同じ結果が得られる。
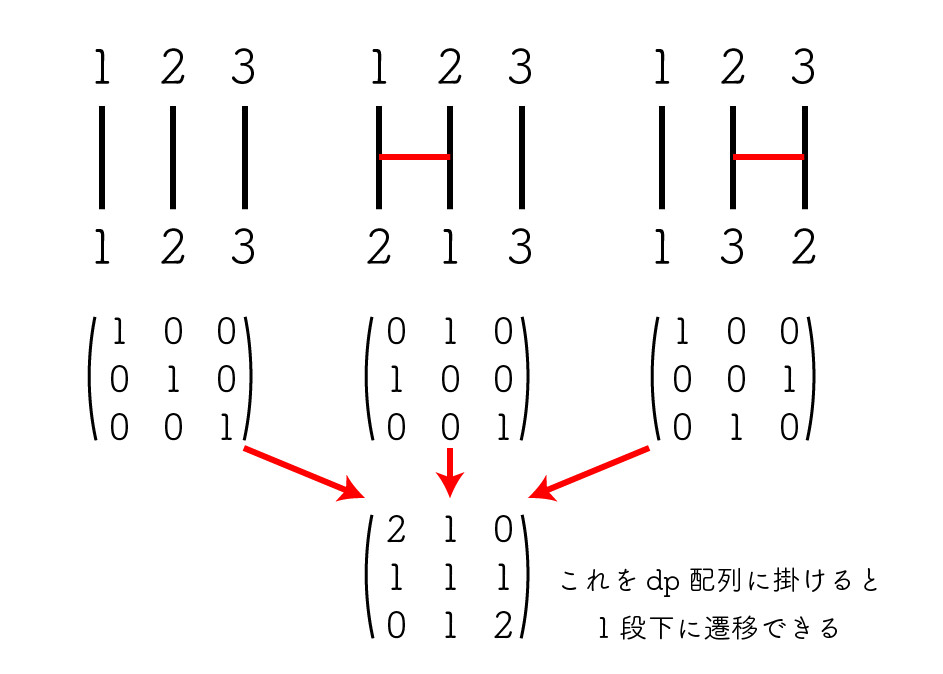
加えて、この行列の総和は段数 $i$ に依存しない。この行列の総和を $M$ とおくと、
$$
dp_{H} = M^H dp_0
$$
となる。なお $dp_0$ は定義から、第 1 成分が 1 で他は全て 0 のベクトルである。
求める答えは $dp_{H, K}$ なので、これは行列 $M^H$ の $(K, 1)$ 成分となる。
あみだくじの数と Fibonacci 数列
まずは $M$ を求めたい。横線の全パターンを全探索すれば $O(W 2^W)$ で求まるが、工夫すれば $O(W)$ で求めることができる。
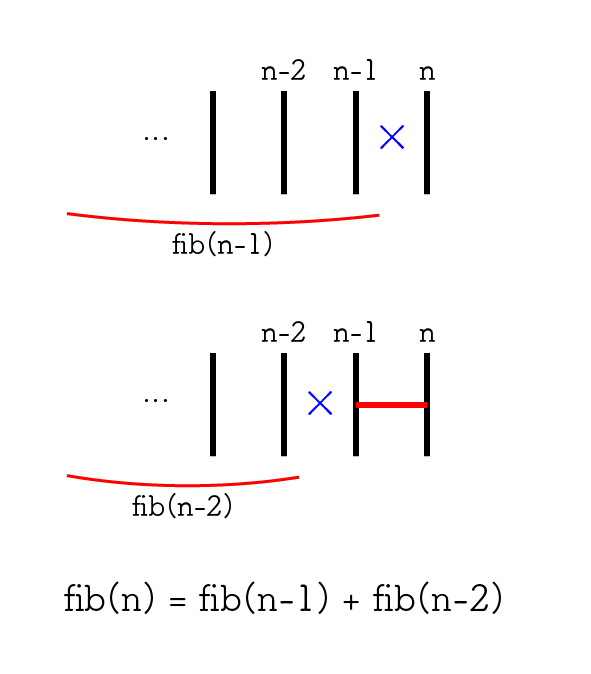
鍵となるのは、「縦線 $n$ 本のあみだくじにおける横線のパターン数は $F_n$」という法則である。ここで $F_n$ は Fibonacci 数列 の第 $n$ 項である。
これは数学的帰納法で示せる。以下の図のように、 $n$ 本目と $n-1$ 本目の間に線を引くか否かで場合分けすればよい。
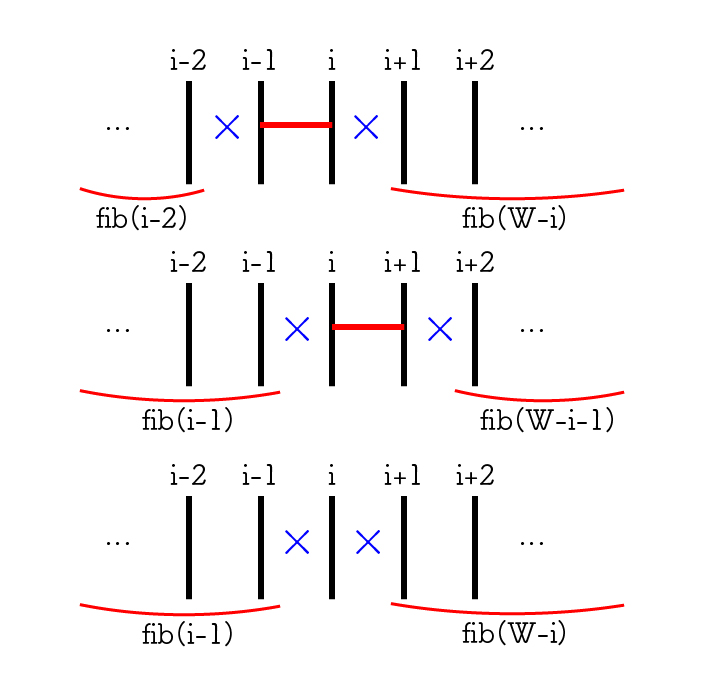
定義から、 $M_{i, j} =$ 「$i$ が $j$ に行き着くような、横線の配置数」である。段数が 1 なので、 $|i - j| \gt 1$ なら $M_{i, j} = 0$ となる。そうでない場合は、下の図のようにして求められる。
行列の累乗
後は行列 $M^H$ を計算すればいい。普通に計算すると、
- 行列同士の積の計算量は $O(W^3)$
- これを $H$ 回繰り返す
より、計算量は $O(W^3 H)$ となる。しかし、 繰り返し二乗法 を用いれば $O(W^3 \log H)$ 時間に高速化できる。
繰り返し二乗法とは、
- $H$ が奇数なら $M^{H - 1}M$ にバラす
- $H$ が偶数なら $\left({M^2}\right)^{H/2}$ に圧縮する
といった具合に再帰的に累乗を求めるアルゴリズムのことを指す。これで指数が高々 2 回毎に半分になるため、計算回数を $O(\log H)$ に落とせる。
実装例
提出 #34713346 - AtCoder Beginner Contest 113
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
|
#include <iostream>
#include <vector>
using namespace std;
using ll = long long;
const ll MOD = 1e9 + 7;
ll fib[1000];
// Fibonacci数列を埋める
void precalc() {
fib[0] = 1;
fib[1] = 1;
for(int i = 2; i < 1000; ++i) {
fib[i] = (fib[i - 1] + fib[i - 2]) % MOD;
}
return;
}
// 正方行列の積
vector<vector<ll>> matmul(vector<vector<ll>> a, vector<vector<ll>> b) {
int l = a[0].size();
vector<vector<ll>> ret(l, vector<ll>(l, 0));
for (int i = 0; i < l; ++i) {
for (int j = 0; j < l; ++j) {
for (int k = 0; k < l; ++k) {
ret[i][j] += a[i][k] * b[k][j];
ret[i][j] %= MOD;
}
}
}
return ret;
}
// ダブリングによる行列累乗
vector<vector<ll>> matpow(vector<vector<ll>> m, int n) {
int l = m[0].size();
// 単位行列を返す
if (n == 0) {
for (int i = 0; i < l; ++i) {
for (int j = 0; j < l; ++j) {
m[i][j] = (i == j);
}
}
return m;
}
if (n == 1) return m;
if (n % 2) {
return matmul(matpow(m, n - 1), m);
} else {
return matpow(matmul(m, m), n / 2);
}
}
int main() {
// Fibonacci数列を先に求める
precalc();
int H, W, K;
cin >> H >> W >> K;
--K;
vector<vector<ll>> M(W, vector<ll>(W, 0));
// 以降Mは0-indexedであることに注意
// 左に移動するパターン
for (int i = 2; i <= W; ++i) {
M[i - 2][i - 1] = fib[i - 2] * fib[W - i] % MOD;
}
// 右に移動するパターン
for (int i = 1; i <= W - 1; ++i) {
M[i][i - 1] = fib[i - 1] * fib[W - i - 1] % MOD;
}
// 真下に移動するパターン
for (int i = 1; i <= W; ++i) {
M[i - 1][i - 1] = fib[i - 1] * fib[W - i] % MOD;
}
auto res = matpow(M, H);
cout << res[K][0] << endl;
return 0;
}
|



