この記事は TSG Advent Calendar 2018 の 10 日目の記事として書かれたものです。
私は東京大学の TSG(理論科学グループ)というサークルに所属しているのですが、TSG は今年の駒場祭1で「TSG LIVE! 2」という企画を 3 日に渡って開催しました。
TSG の部員達が「競プロ」「AI 実装」「コードゴルフ」「CTF」を実際にやる様子を生放送で実況するというもので、私はそのうち「競プロ」「AI 実装」でプレイヤーとして参加しました。本記事はそのうち「競プロ」の方について語ります。
なお一口に競プロと言いましたが、今回行われたのは「アルゴリズム」ではなく「マラソン」でした。とはいえ時間が 75 分なのでマラソンの中ではとても短い部類ではありました2。
問題 「イワシの収穫祭」
壁がまばらに配置されている $H \times W$ のグリッドがある。
fiord くんは最初、このグリッドのどこか一点に存在する。そこから毎ターンいずれかの方向へ 1 マスずつ移動する(あるいは移動しない)ことで、 $T$ ターンに渡って $N$ 匹の「イワシ」を収穫する。
各イワシは特定のターンにグリッド上に生えてくる。そして毎ターン、 fiord くんか他のイワシの中で、自分に最も近いものに近づくように 移動する(細かい動き方は割愛)。なおイワシは複数体が同一のマス上に存在することができる。これを「群れ」と呼ぶことにする。
fiord くんはイワシの群れに接触することでイワシを回収できる。しかしイワシは集団になると凶暴になる性質がある。fiord くんは 6 体以上のイワシの群れに接触すると、回収できない上に怪我をして 5 ターン行動不能になる。
最初にグリッドの配置と各イワシの出現するターン及び位置が与えられる。このとき、fiord くんの動きを出力せよ。
制約と点数
- 全ケース共通
- $H = W = 22$
- tiny (1 ケース)
- $N = 50$
- $T = 150$
- 壁は全体の $15\%$
- little (6 ケース)
- $N = 250$
- $T = 1000$
- 壁は全体の $25\%$
- much (6 ケース)
- $N = 3000$
- $T = 1000$
- 壁は全体の $25\%$
- challenge (3 ケース)
- $N = 1000$
- $T = 1000$
- 壁は全体の $47.5\%$ 、作為的に生成
challenge のケースは以下のようになっており、盤面が実質直線になっている。
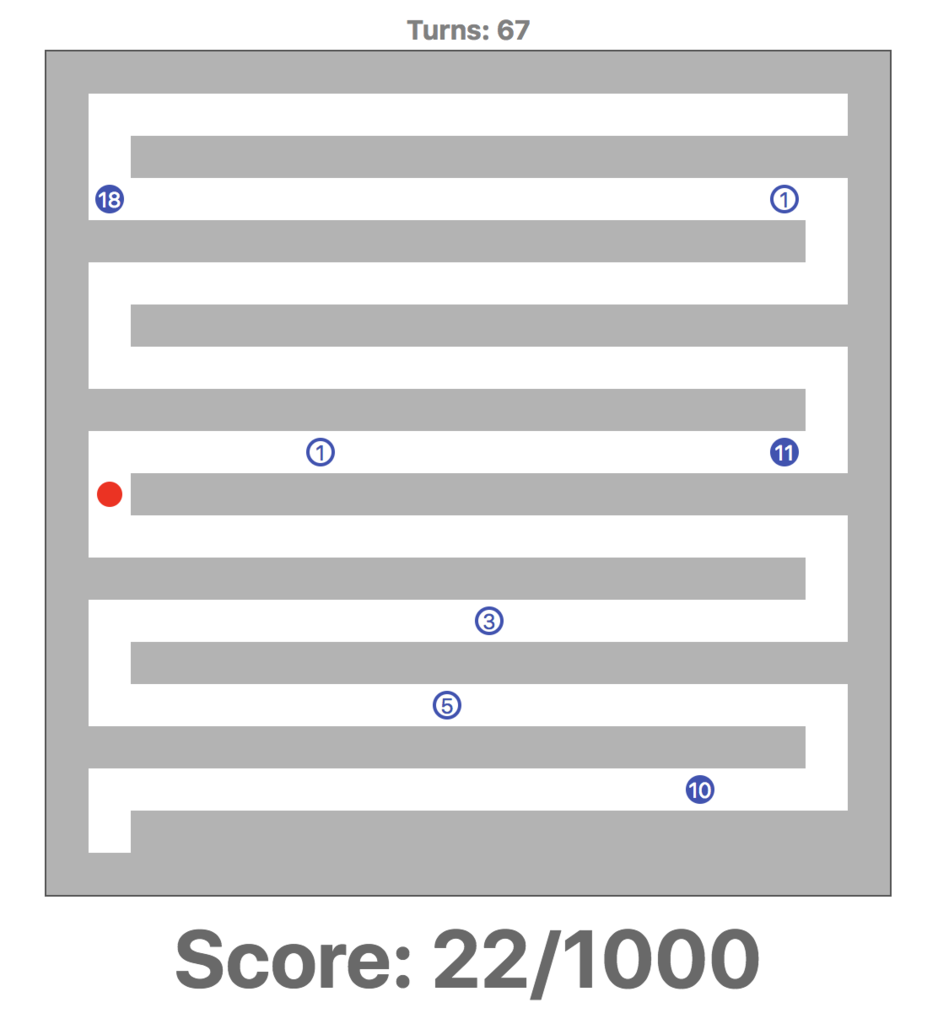
各ケースごとにイワシの収穫率がそのままスコアとなり、その合計が最終スコアとなる。
本番の流れ
事前に fiord さんから聞いていたので覚悟はしていましたが、まぁまぁ問題文が長い。特にイワシの動きの部分が曲者なのですが、「一番近い fiord くんとイワシに近づく」ということだけ頭に入れて読み流しました。実はサンプルコードに動きをシミュレートするコードが入っているので、イワシの動きが細かく分からなくてもなんとかなりました。
乱択厳選
マラソンということで、最初にしたのが乱択です。ランダムに方向を出力して、実際にシミュレートします。
しかしここで競プロ er にあるまじきミス。fiord くんの移動は自身でシミュレートするのですが、その際に壁判定と場外判定を両方飛ばしまいました。結果として範囲外参照が出たり出なかったりすることになり、しばらく唸っていました。
それに気づいてバグを修正したのが大体 25 分頃。そこから少しだけ工夫をして、この生成を 7 回繰り返して最適なやつを選択するコードを提出したのが 35 分頃でした。
しかしこのスコアが 4.99 点とあまり芳しくありませんでした。なぜか前に出したバグ有り乱択の方が 5.29 点とスコアが高いという有様。この時点で対戦相手の dai さんは 5.73 点を出しており、内心焦っていました。
中心へ
ここで初めてビジュアライザを起動。すると、想像していた以上にイワシが fiord くんへ吸い寄せられていることが分かりました。
「これ下手に動かない方が良いのでは?」と勘付き、試しに一度も動かないコードを提出してみると 5.56 点と最高記録が出ました3。
そして特にスコアが高かったやつ( これ )をビジュアライザで眺めていると、「グリッドの中心に近いほどイワシが効率的に吸い寄せられるのではないか」と思い始めました。以降それを実装することになります。
逆辺張り BFS
後は中心へ移動するプログラムを組むだけです。具体的には「逆辺張り BFS」をします。
まず fiord くんの初期位置を始点として BFS(幅優先探索)をします。このとき、「どの方向の移動によってそのマスへ移動したか」を同時に記録します。
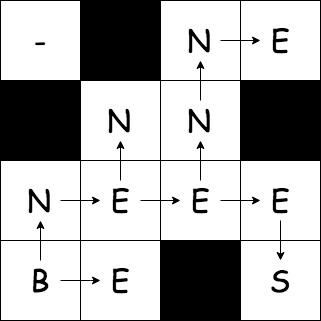
次に目的地を決めます。今回は到達可能な中で $(H / 2, W / 2)$ とのマンハッタン距離が一番小さい場所を目的地にしました。
最後に経路を求めます。今度は目的地を始点として、先程の遷移を逆走するようにします。すると最終的には fiord くんの初期位置へたどり着きます。その際通った文字を反転させれば、これが目的地へ移動するような文字列になるわけです。以下の例では NEENN がそれに当たります。
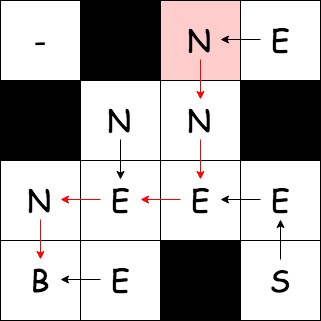
このアルゴリズムを思いつくのは秒なのですが、実装に地味に時間がかかりました。その根底のミスが「queue への push し忘れ」というしょうもないもので、これに気づかないまま終わっていたら競プロ引退案件でした。
それでもなんとかそれに気づいて終了 2 分前に提出。これが無事バグ 0 で真ん中へ移動してくれて、6.38 点という最高得点を叩き出しました。
結果
最終結果は私のスコアが最終提出の 6.38 点、dai さんのスコアが最初の提出の 5.73 点でなんとか勝つことができました。
後でコードを読んだところ、dai さんは「10 手先読み」を実装していたようです。具体的には、「あと $n$ 手ある状態で各方向へ移動した場合の最高スコア」を再帰的に求めて、一番いい方向へ動くというものです。
ただし今回の問題はシミュレーションにとても時間がかかるため、TLE(15sec 超過)になっていたことに気づかなかったそうです。それにしてもあれだけの量を 75 分で実装していたのは驚嘆という他ありません。
想定解法
ライブ終了後、fiord さんに想定解法を訊いたところ「 影響マップ 」という単語が出てきました。
今回の問題を例にとります。fiord くんはできるだけイワシを収穫したいので、当然ながらイワシに近づきたいことになります。一方で 6 匹以上のイワシの群れには当たると怪我してしまうため、できるだけ近づきたくありません。
そこで、5 匹以下のイワシの群れからは「 正のオーラ 」、6 匹以上の群れからは「 負のオーラ 」が周り全体へ広がっていると考えます。これらのオーラは発信源から遠くへ行くほど小さくなり、重ね合わせると互いに打ち消し合います。そして全てのオーラを重ね合わせたとき、一番正のオーラが強い方に移動すると得ということになるわけです。
これが「影響マップ」という考え方だそうで、「なるほど確かに実装も楽そうだなぁ」と思いました。マラソンと言えば「焼きなまし法」と「ビームサーチ」しか知らなかったので、良い知見が得られました。
反省
マラソンと言っておきながら最終的には「真ん中に移動するだけ」になりましたが、それはそれで競プロらしくて良いんじゃないかなと思います。 ただ範囲外参照や BFS のバグについては要反省ですね。緊張して大分焦ってコードを生んでいたので、もう少し落ち着きを持てるようになりたいです。
マラソンも楽しいのですが、次に TSG LIVE があれば作問に挑戦してアルゴリズムも開きたいなぁと思いました。 アルゴリズム勢は TSG にもそれなりにいるので楽しそうです。