概要
縦 $N$ マス横 $M$ マスのグリッドに、
- 縦 1 マス横 2 マスのタイル $A$ 枚
- 縦 2 マス横 1 マスのタイル $B$ 枚
を重ねたり回転させたりせずに敷き詰めることは可能か。可能ならば敷き詰め方の例を出力せよ。
制約
- $1 \leq N, M \leq 10^3$
- $0 \leq A, B \leq 5 \times 10^5$
解説
$N$ と $M$ の偶奇で場合分けする。
1. $N, M$ が共に偶数の場合
この場合、以下のようにグリッドを 2×2 の小さい領域に分割して、それぞれに同じ種類のタイルを 2 枚ずつ置くのが最適となる。
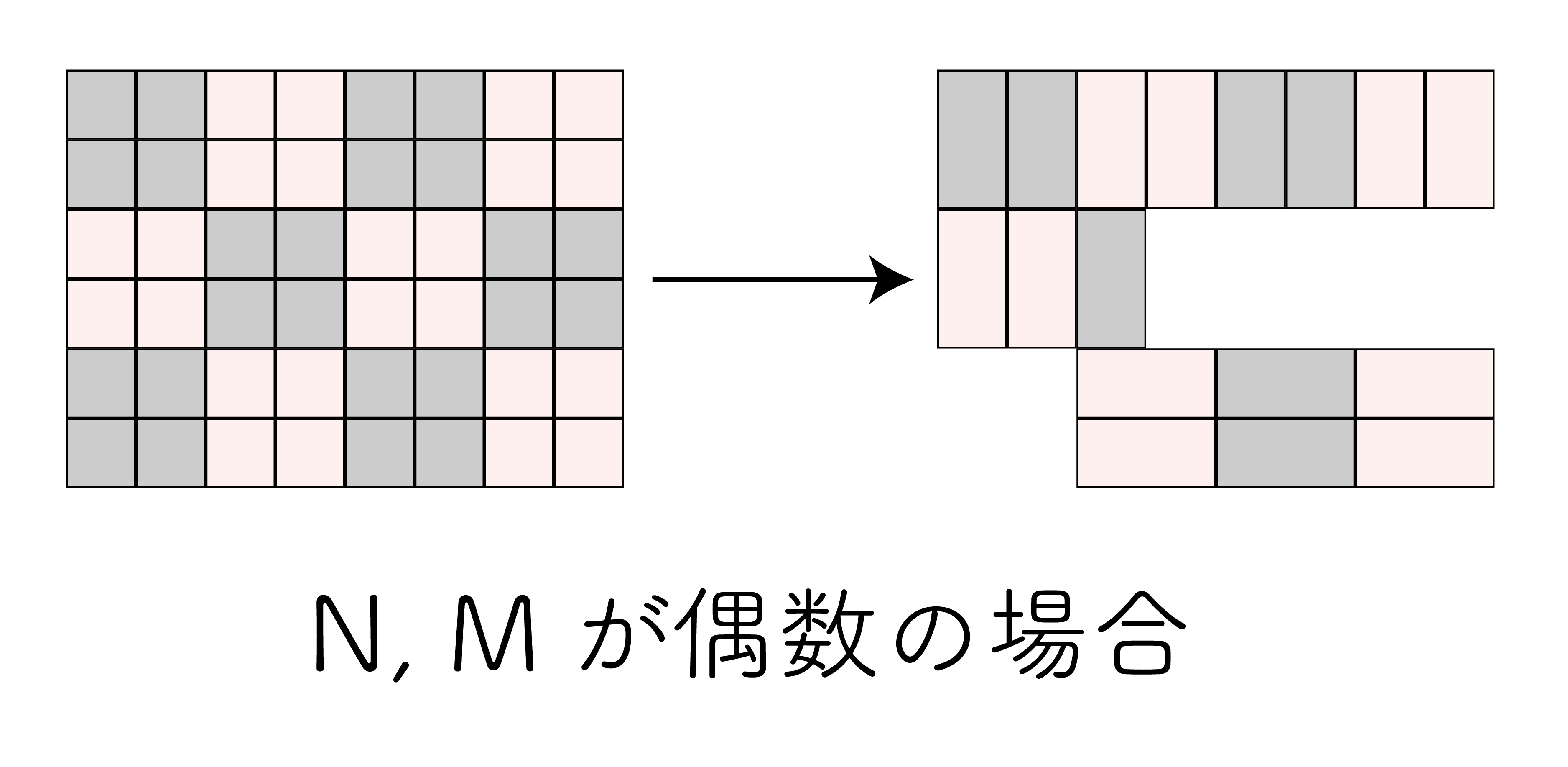
これが可能な条件は $NM \geq 4 \left( \lceil A / 2 \rceil + \lceil B / 2 \rceil \right)$ である。
2. $N, M$ の一方が奇数の場合
この場合もさっきと大差はなく、下のように端の行か列を先に埋めてしまって 1 のケースに帰着させるだけで OK。
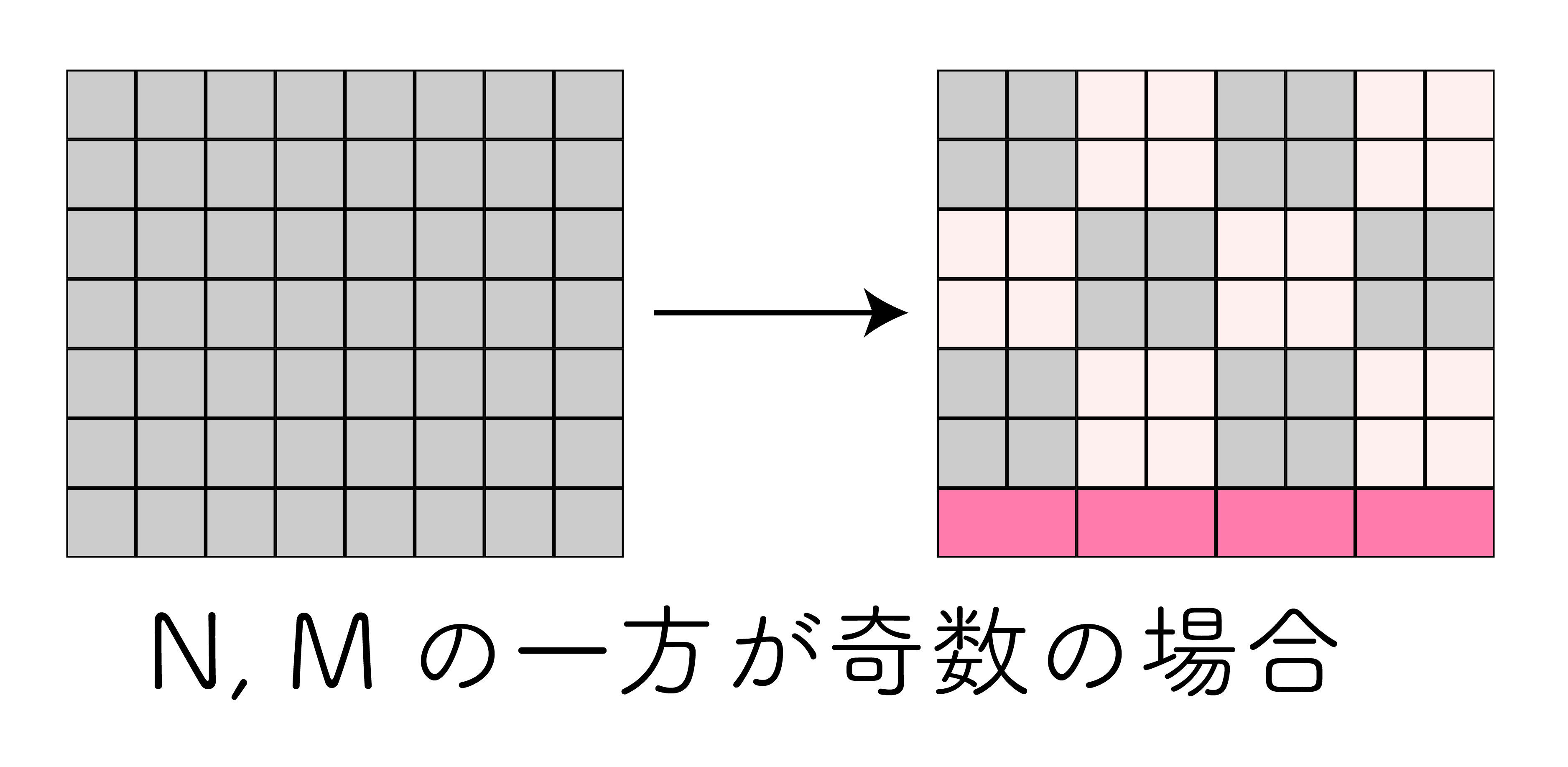
3. $N, M$ が共に奇数の場合
この場合も端の行と列を先に埋めれば 大抵の 場合上手くいく。 ただし、余った 1 マスが原因でコーナーケースが生じる。それが「残った $A, B$ が共に奇数の場合」である。
このとき $A, B$ でそれぞれ余った 1 個のタイルが 2 個分の領域を占めることになるが、実は画像下のように余ったタイルを 1 つの領域にねじ込むことができる。
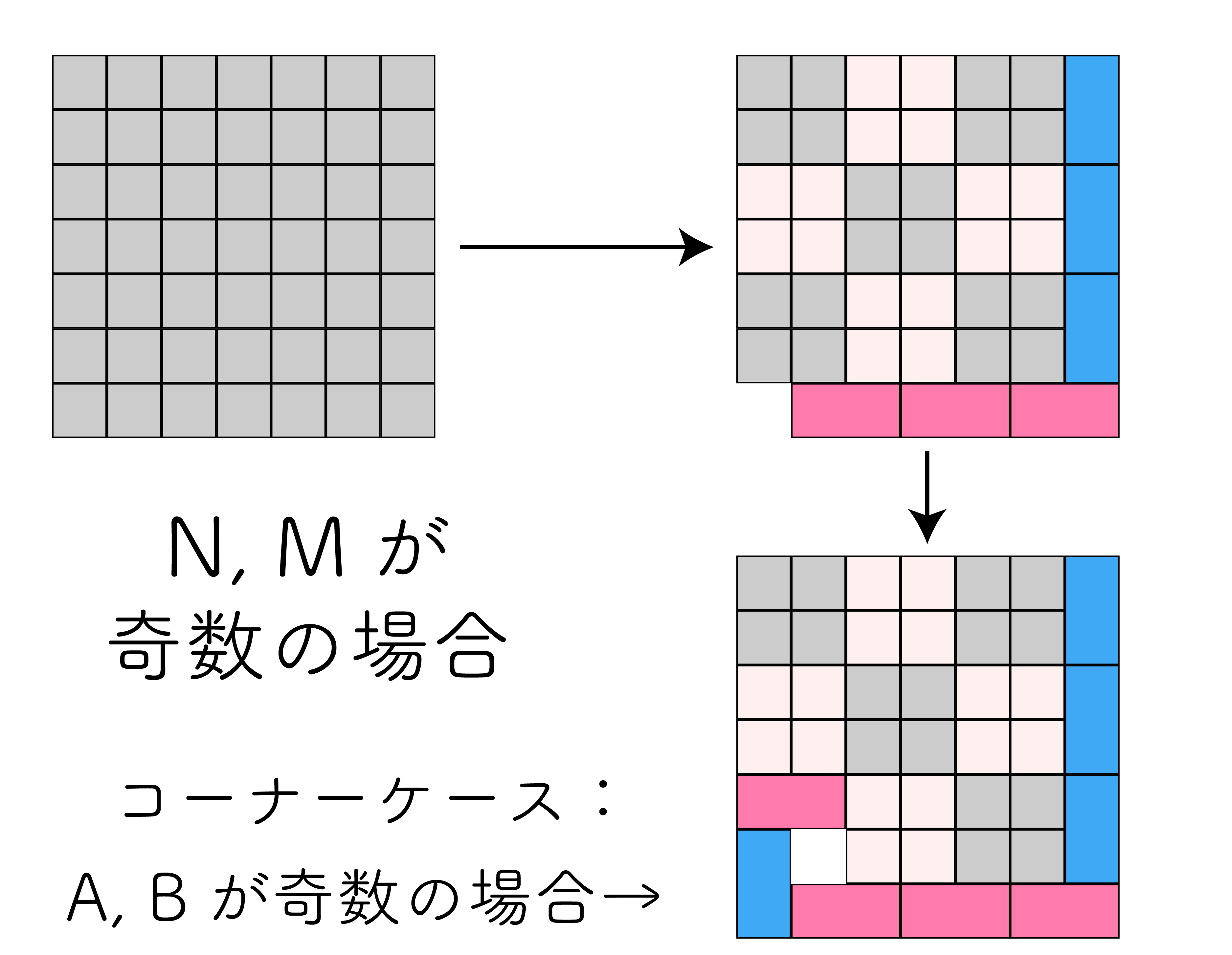
実装例
以上を全て考慮してグリッドを埋めれば AC なのだが、いかんせん実装が難しい。 私が書いたコードもコピーだらけで正直あまり見せたくないので、見たい人は以下のリンクを踏んでください。