N - 木
問題
$n$ 頂点の木をなす辺集合 $E$ が与えられる.
これから $n$ 頂点 $0$ 辺のグラフに $E$ の辺を追加していくことで木を作る.ただし追加する過程でグラフの辺は常に連結でなくてはならない.
辺を追加する順番の通り数を求めよ.
制約
考察
最初に追加する辺を決めると,辺の選ぶべき順序関係から,辺を頂点,関係を辺とする根付き木が構成できる.下図のような感じ.
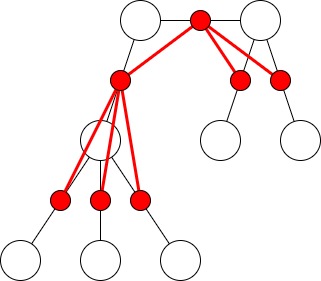
後はこの新しいグラフの頂点を選ぶ順番の通り数を求めればいいが,これは DFS と多項係数によってできる.
例えば根が 3 つの子を持っていて,その部分木のサイズが $s_1, s_2, s_3$ だったとする.このとき最初に根を塗れば後は各部分木内で制約を満たしてさえいればいい.よって以下のようにして順番を決められる.
- 赤,青,緑のボールをそれぞれ $s_1, s_2, s_3$ 個用意する.
- これらを好きな順番に並び替える.
- 各色のボールに,対応する部分木の頂点を選んだ順番に書き込む.
2 の並べ方の数は多項係数で求められて,3 は子の部分木の通り数を DFS で求めて掛け合せればいい.
実装例
木の生成は BFS によって行った.このときトポロジカル順序が自然に求まるので,後で DFS するときにそれを使っている.
提出 #9680521 - Typical DP Contest
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
|
#include <iostream>
#include <vector>
#include <queue>
template <class Cost = int>
struct Edge { ... };
template <class Cost = int>
using Edges = std::vector<Edge<Cost>>;
template <int MOD>
struct ModInt { ... };
constexpr int MOD = 1e9 + 7;
using mint = ModInt<MOD>;
template <class T>
struct Combination { ... };
const Combination<mint> C(10000);
void solve() {
int n;
std::cin >> n;
int m = n - 1;
Edges<> edges;
std::vector<std::vector<int>> es(n);
for (int i = 0; i < m; ++i) {
int u, v;
std::cin >> u >> v;
--u, --v;
es[u].push_back(i);
es[v].push_back(i);
edges.emplace_back(u, v);
}
mint ans = 0;
for (int r = 0; r < m; ++r) {
std::vector<std::vector<int>> chs(m);
// BFSで木を構成
// このときついでに逆トポロジカル順序も求める(stk)
std::queue<int> que;
que.push(r);
std::vector<bool> used(m, false);
used[r] = true;
std::vector<int> stk;
while (!que.empty()) {
int e = que.front();
que.pop();
stk.push_back(e);
int v;
v = edges[e].src;
for (auto f : es[v]) {
if (used[f]) continue;
chs[e].push_back(f);
que.push(f);
used[f] = true;
}
v = edges[e].dst;
for (auto f : es[v]) {
if (used[f]) continue;
chs[e].push_back(f);
que.push(f);
used[f] = true;
}
}
std::vector<int> sz(m);
std::vector<mint> pat(m);
// 逆トポロジカル順序を使って非再帰DFS
while (!stk.empty()) {
int e = stk.back();
stk.pop_back();
sz[e] = 0;
pat[e] = 1;
for (auto f : chs[e]) {
sz[e] += sz[f];
pat[e] *= pat[f];
}
int z = sz[e];
for (auto f : chs[e]) {
pat[e] *= C.comb(z, sz[f]);
z -= sz[f];
}
++sz[e];
}
ans += pat[r];
}
std::cout << ans << std::endl;
}
|
