この記事は ISer Advent Calendar 2018 の 15 日目の記事として書かれたものです。

機能と計算量

簡潔ビットベクトルとは、与えられた長さ $N$ の bit 列に対して以下の操作を実現するデータ構造である。

そして必要な空間計算量は $N + o(N)$ bit となる。

select を $O(1)$ に落とすことも可能らしいが、実装が重いらしいためここは一般に妥協されている。

それ累積和でよくね？

実のところ、上の機能を実現したいだけなら「累積和¹」を使えば事足りる。これも上の機能を同様の時間計算量で実現できる上に、実装が非常に楽。

しかし簡潔ビットベクトルには累積和を上回るポイントがある。それが「 空間計算量 」である。

bit 列の累積和の空間計算量は $O(N)$ と捉えられがちだが、厳密に評価すると $N \lg N$ bit²となる。この $\lg N$ は何かと言うと、累積和の値を保持するのに必要な bit 数である。

例えば bit 列の長さが $255 = 2^8 - 1$ だったとしよう。このとき累積和の各値は $8$ bit 符号なし整数で保持すればよい。これは $8$ bit 符号なし整数の値域が $[0, 2^8)$ だからだ。

これと同様の理屈で、長さ $N$ の bit 列の累積和は $\lg N$ bit 整数を使う必要がある。よって全体で $N \lg N$ bit が必要となる³。

かたや簡潔ビットベクトルはどうかというと、それを考慮した上で空間計算量は $N + o(N)$ となる。

具体的に必要な bit 数を概算すると以下の通り。

所詮 $\log$ が落ちた程度の差なので劇的に小さくなるわけではないが、上のように数倍は小さくはなる。

そういうわけで、「bit 列の累積和を大量に用意したいけど、累積和だとメモリを食いすぎてしまう…」という場合⁴に役に立つ。

rank の仕組み

簡潔ビットベクトルの実装でメインとなるのは rank である。逆にこれさえ実装できれば完成したも同然となる。 というのも access は元のデータを参照するだけ、 select は rank によって二分探索すればいいからだ。

そういうわけでこれらは実装例に載せる程度に抑え、以降 rank の仕組みに重点を置いて話すことにする。

まず rank の仕組みは、「 平方分割 」という技法を念頭に入れておくとより理解しやすいように思われるので、そちらを先に説明する。

平方分割

「平方分割」とは、長さ $N$ の数列を長さ $\sqrt N$ の数列 $\sqrt N$ 個に分割することで計算量を減らす技法である。

以下は長さ $16$ の数列の区間和を求める際に、平方分割を適用した例である。このように区間を「スキップする」感覚で、前計算 $O(N)$ で計算量を $O(\sqrt N)$ に落とすことができる。

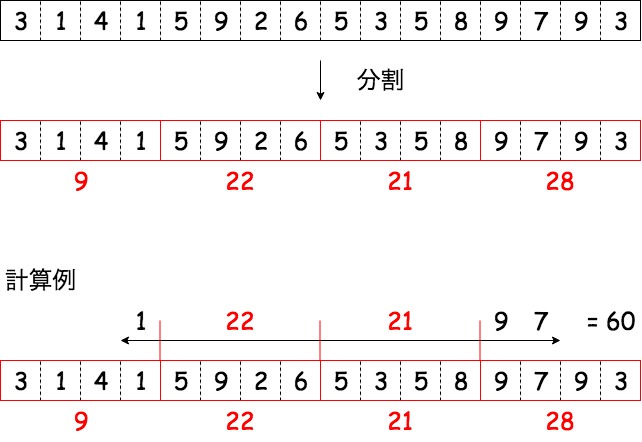
chunk と block

これと同様にビットベクトルも bit 列をブロックに分割するのだが、平方分割と違って 2 段階に分割する。

まずは「chunk⁵」という大ブロックに分割する。そして各 chunk の境界に、そこまでに現れた 1 の個数の合計を記録しておく。 先程の平方分割と違い、今回はそこまでの全区間の合計であることに注意。

そして次に各 chunk を「block⁶」という小ブロックに分割する。こちらも保持するデータは chunk と同様だが、各 chunk 毎に独立となる。

具体例としては以下のようになる。

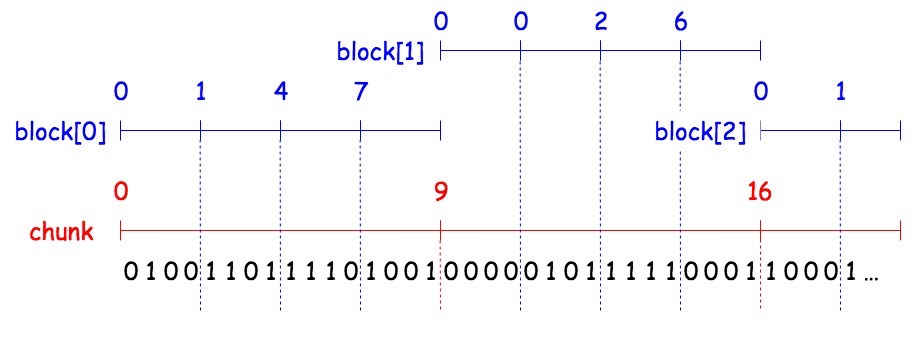
このデータによって、 rank は以下のように計算できる。要領は平方分割と同じ。

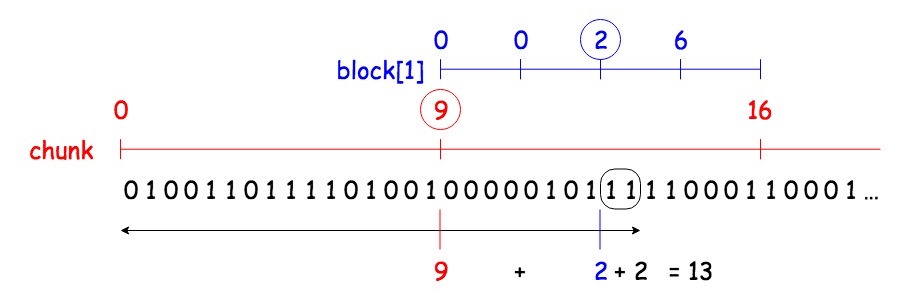
後に示すように、chunk と block の幅 $(c, b)$ は $((\lg N)^2, (\lg N) / 2)$ に設定すると、簡潔性が満たされる。 ただし実装する場合は、この幅を $N$ に応じて変えることまではしなくていい。想定している最大ケースに合わせればいいだろう。

popcount

上図にて黒で囲まれた bit 列の処理(通称 popcount)だが、愚直にやる場合 $O(b)$ かかってしまう。

ここの計算量を減らす方法は主に 3 つある。

1. 「bit パターン」と「1 の数」を対応させるテーブルを作っておく。 理論的にはこれが最善で $O(1)$ 。少し実装が面倒なので実用上はあまり使われていないらしいが、今回は理論を重視するためにこれで実装する。

2. __builtin_popcount⁷ のように、プログラミング言語に既に実装されている関数を使う。

3. シフト演算を上手く使う。詳細は省くが、シフト演算で上手いことやると $O(\log w)$ での popcount を自力で実装することができる。

簡潔性の証明

それでは厳密な空間計算量を計算することで、簡潔ビットベクトルの簡潔性を示す。特に興味がなければ実装例に移っていただいて構わない。

まず先に述べた通り、chunk と block の幅 $(c, b)$ は $((\lg N)^2, (\lg N) / 2)$ とする。このとき、各補助変数に必要な空間計算量は以下のようになる。

元データ

これは普通に $N$ bit 必要となる。

chunk

chunk の数は全部で $N / c$ 個。各値は $N$ を上回らないので、 $\lg N$ bit 整数で保持することになる。よって必要な bit 数は、

$$ \dfrac{N}{(\lg N)^2} \times \lg N = \dfrac{N}{\lg N} $$

より $\dfrac{N}{\lg N}$ bit となる。

block

block の数は全部で $N / b$ 個。各値は $c$ を上回らないので、 $\lg c = 2 \lg (\lg N)$ bit 整数で保持することになる。よって必要な bit 数は、

$$ \dfrac{N}{(\lg N) / 2} \times 2 \lg (\lg N) = \dfrac{4 N \lg (\lg N)}{\lg N} $$

より $\dfrac{4 N \lg (\lg N)}{\lg N}$ bit となる。

table

最後に popcount で参照する table。block の bit パターンは計 $2^b = \sqrt{N}$ 通り。各値は $b$ を上回らないので $\lg b = \lg (\lg N) - 1$ bit 整数で保持することになる。よって必要な bit 数は $\sqrt{N} (\lg (\lg N) - 1)$ bit となる。

合計

以上を合計すると、簡潔ビットベクトルが必要とする空間計算量は

$$ \begin{aligned} & N + \frac{N}{\lg N} + \frac{4 N \lg (\lg N)}{\lg N} + \sqrt{N} (\lg (\lg N) - 1) \\ = & N \left( 1 + \frac{1}{\lg N} + \frac{4 \lg (\lg N)}{\lg N} + \frac{\lg (\lg N) - 1}{\sqrt{N}} \right) \end{aligned} $$

bit となる。 $\dfrac{1}{\lg N}, \dfrac{4 \lg (\lg N)}{\lg N}, \dfrac{\lg (\lg N) - 1}{\sqrt{N}}$ はそれぞれ $N \to \infty$ で $0$ に収束するため、これはランダウ記号で $N + o(N)$ bit と表すことができる。以上より簡潔性が示された。 $\square$

実装

上の仕組みが理解できれば後は実装だけなのだが、これが意外と難しい。以下では個人的に詰まりやすかった箇所について軽く解説する。

元データの持ち方

まず問題となるのが「元データの保持方法」である。

bool の配列として持てば一見無駄がないように思われる。しかし C++における bool のサイズは環境依存で、大抵は 1byte らしい。これでは 8 倍損してしまう。

そこで今回は、unsigned char(8bit 符号なし整数)の配列として元データを表現している。 data[i] >> k & 1 で元データの下から $8i + k$ bit 目が求まる、といった次第である。ここの幅は block に合わせると実装がしやすくなる。

初期化方法

bit 列の初期化方法といっても、

• 上のように配列として与える
• 0 と 1 からなる文字列として与える

などの様々な方法がある。今回はこれらのどれが来ても対応できるように、「初期化時点では長さのみ指定して、後からデータを書き換える」という方式にした。全部データを書き換え終わったら、 build() を呼んで前計算をしてもらう。

ただこの方法には大きな難点がある。それが「build() の呼び忘れ」である。本当に呼び忘れるので使うときは注意してほしい。

index

実装していると否が応でも 0-indexed か 1-indexed か困ることになる。1-indexed にすると access が実装しづらくなり、0-indexed にすると rank が「先頭から $n + 1$ bit の 1 の数」と微妙な感じになる。

これを解決する方法として、以下では rank を「半開区間 $[0, n)$ に含まれる 1 の数」としている。これなら全体を 0-indexed に統一できて、かつ rank の意味も自然になる。さらに rank の実装も地味に楽になる。

実装例

以下の実装は $N \lt 2^{16}$ としている。

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114

#include <vector>

using namespace std;

using u8 = unsigned char;
using u16 = unsigned short;

class BitVector {
  u16 length, cnum, bnum;
  // bit列の長さ、chunk数、chunk毎のblock数

  static const int cw = 256, bw = 8;
  // chunkの幅、blockの幅

  vector<u8> bit;  // 元データ
  vector<u16> chunk;
  vector<vector<u8>> blocks;
  static const vector<u8> table = {
    0, 1, 1, 2, 1, 2, 2, 3, 1, 2, 2, 3, 2, 3, 3, 4,
    1, 2, 2, 3, 2, 3, 3, 4, 2, 3, 3, 4, 3, 4, 4, 5,
    1, 2, 2, 3, 2, 3, 3, 4, 2, 3, 3, 4, 3, 4, 4, 5,
    2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6,
    1, 2, 2, 3, 2, 3, 3, 4, 2, 3, 3, 4, 3, 4, 4, 5,
    2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6,
    2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6,
    3, 4, 4, 5, 4, 5, 5, 6, 4, 5, 5, 6, 5, 6, 6, 7,
    1, 2, 2, 3, 2, 3, 3, 4, 2, 3, 3, 4, 3, 4, 4, 5,
    2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6,
    2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6,
    3, 4, 4, 5, 4, 5, 5, 6, 4, 5, 5, 6, 5, 6, 6, 7,
    2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6,
    3, 4, 4, 5, 4, 5, 5, 6, 4, 5, 5, 6, 5, 6, 6, 7,
    3, 4, 4, 5, 4, 5, 5, 6, 4, 5, 5, 6, 5, 6, 6, 7,
    4, 5, 5, 6, 5, 6, 6, 7, 5, 6, 6, 7, 6, 7, 7, 8,
  };  // 理想は3bit整数だが、そんなものはないので妥協

public:
  explicit BitVector(int N) : length(N) {
    cnum = (length + cw - 1) / cw;
    bnum = cw / bw;

    bit.assign(cnum * bnum, 0);
    chunk.assign(cnum + 1, 0);
    blocks.assign(cnum, vector<u8>(bnum, 0));
  }

  /** pos bit 目を b に変える */
  void set(int pos, u8 b) {
    int bpos = pos / bw;
    int offset = pos % bw;

    if (b == 0) {
      bit[bpos] &= ~(1 << offset);
    } else if (b == 1) {
      bit[bpos] |= (1 << offset);
    }
  }

  /** pos bit 目を返す */
  u8 access(int pos) const {
    int bpos = pos / bw;
    int offset = pos % bw;
    return bit[bpos] >> offset & 1;
  }

  /** numの立っているbit数を返す */
  u8 popCount(u8 num) const {
    return table[num];
  }

  /** 前計算 chunk と blocks を適切に埋める */
  void build() {
    chunk[0] = 0;
    for (int i = 0; i < cnum; ++i) {
      blocks[i][0] = 0;
      for (int j = 0; j < bnum - 1; ++j) {
        blocks[i][j + 1] = blocks[i][j] + popCount(bit[i * bnum + j]);
      }
      chunk[i + 1] = chunk[i] + blocks[i][bnum - 1] + popCount(bit[(i + 1) * bnum - 1]);
    }
  }

  /** [0, pos) にある 1 の数を返す */
  int rank(int pos) const {
    int cpos = pos / cw;
    int bpos = pos % cw / bw;
    int offset = pos % bw;

    // 余った部分から、必要な部分だけをbitmaskで抽出する
    u8 masked = (bit[cpos * bnum + bpos]) & ((1 << offset) - 1);
    return chunk[cpos] + blocks[cpos][bpos] + popCount(masked);
  }

  /**
   * rank(idx)=num なる最小の idx を返す
   * そもそも 1 が num 個なかったら -1 を返す
   */
  int select(int num) const {
    if (num == 0) return 0;
    if (rank(length) < num) return -1;

    int ok = length, ng = 0;
    while (ok - ng > 1) {
      int mid = (ok + ng) / 2;
      if (rank(mid) >= num) {
        ok = mid;
      } else {
        ng = mid;
      }
    }

    return ok;
  }
};

参考リンク

• 完備辞書（簡潔ビットベクトル）の解説 - アスペ日記
  実装の上で一番参考にしたサイト。 rank の解説がむちゃくちゃ丁寧。

• 簡潔データ構造超入門 〜つくって学ぶ簡潔ビットベクトル〜 - EchizenBlog-Zwei
  popcount の項で軽く触れた「シフト演算子で popcount する方法」が載っている。

• 完備辞書 - Eating Your Own Cat Food
  記事の最後にある実装例が非常に参考になった。上の実装例も大半はこれに沿っている。

後書き

データ構造の実装はやってみると結構楽しいし、データ構造への理解も深まるのでオススメです。あと競プロでたまに役に立ちます。

簡潔ビットベクトルは実装難易度としては高い方ではないと思うので、ぜひチャレンジしてみてはいかがでしょうか。