AtCoder Beginner Contest 008 C

C - コイン

概要

整数が書かれたコインが $N$ 枚ある。 $i$ 枚目のコインには $C_i$ が書かれている。

最初にコインの並べ方を $N!$ 通りの中から一様ランダムに 1 つ選び、全て表にして一列に並べる。

その後、左から順にコインを見ていく。今見ているコインに書かれた数字を $C$ とすると、そのコインより右側にあり、かつ $C$ の倍数が書かれているコインを全て裏返す。

全てのコインを見終わった時点で、表になっているコインの枚数の期待値を求めよ。

制約

$1 \leq N \leq 100$
$1 \leq C_i \leq 10^9$

解説

コイン $i$ が最終的に表になる確率を $p_i$ とする。すると期待値の線形性より、最終的に表になるコインの枚数の期待値は $\sum_{i = 1}^N p_i$ で求まる。

コイン $i$ が最終的に表になっているのは、 $C_i$ の約数が書かれたコインが、自分より左に偶数枚あるとき である。 $C_i$ の約数が書かれていないコインは、コイン $i$ の裏表に一切関与しない。よって存在を無視してしまってもよい。

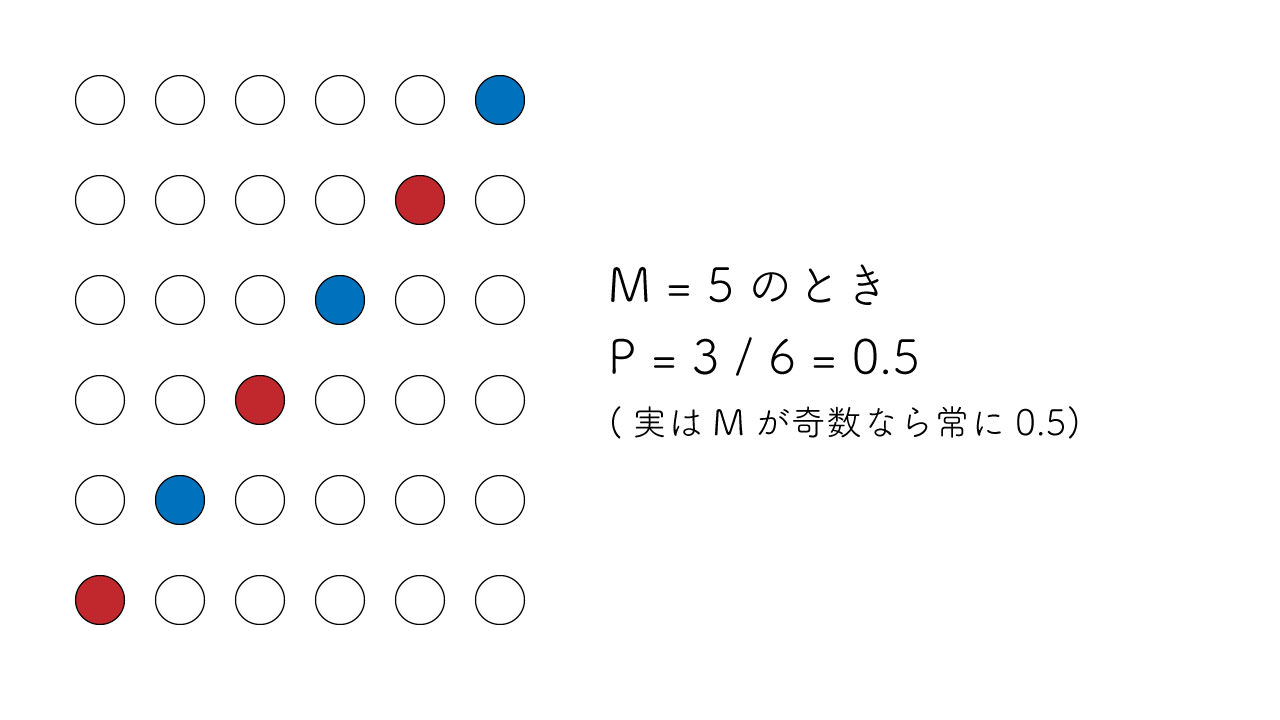
$C_i$ の約数が書かれたコインが、コイン $i$ を除いて $m_i$ 枚あったとする。このときの $p_i$ の値を、図に描いて考えてみる。色がついているのが今見ているコイン(赤なら表、青なら裏)、他の丸は全部その約数が書かれたコインである。

$m_i = 5$ の場合は下図の通り。一般化すると、 $m_i$ が奇数のときは常に $p_i = 0.5$ となる。

$m_i = 6$ の場合は下図の通り。一般化すると、 $m_i$ が偶数のときは $p_i = \dfrac{m_i + 2}{2(m_i + 1)}$ となる。

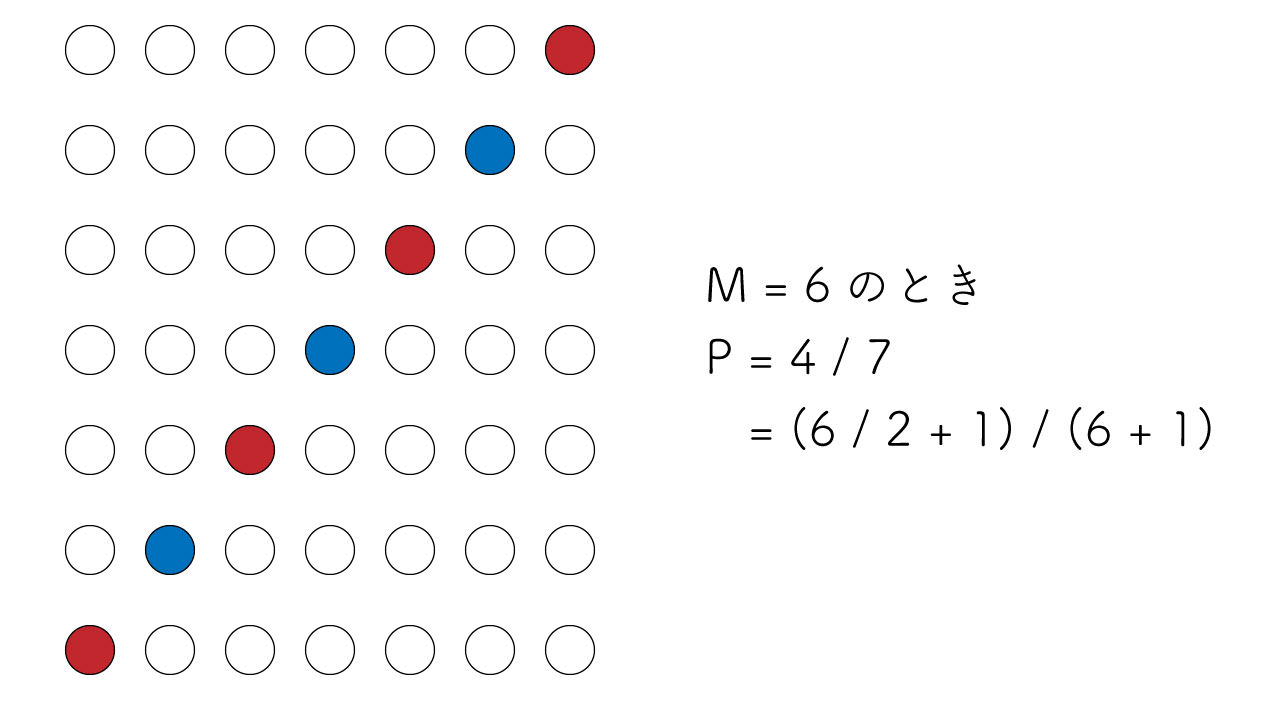
まとめると以下の通り。

$$ p_i = \begin{cases} \frac{1}{2} & (m_i \equiv 0 \pmod{2}) \\ \frac{m_i + 2}{2 (m_i + 1)} & (m_i \equiv 1 \pmod{2}) \end{cases} $$

後はこれらを足していけば答えとなる。

実装例

提出 #2702996 - AtCoder Beginner Contest 008

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60


template <typename T>
using V = vector<T>;
using ll = long long;

#define DOUBLE(n) static_cast<double>(n)
#define REP(i, n) FOR(i, 0, n)

#define fcout cout << fixed << setprecision(10)

/* ---------- ここまでマクロ ---------- */

const ll INF = 1LL << 50;

int main() {
    ll N;
    cin >> N;

    V<ll> C(N);
    REP(i, N) {
        cin >> C[i];
    }
    C.pb(INF);    // 番兵

    SORT(C);

    double ans = 0;
    ll mul = 1;
    // 同じ値がダブっていたとき用

    REP(i, N) {
        if (C[i] == C[i + 1]) {
            mul++;
            continue;
            // 値被りなのでスルー
            // 何もしないとi=N-1でC[N]にアクセスしようとしてセグフォる
            // だが先に追加した番兵によってそれが防がれている
        }

        ll cnt = 0;
        // 自分の約数が書かれたコインを数える
        REP(j, i) {
            if (C[i] % C[j] == 0) cnt++;
        }

        double p;
        // 先程出した確率を実際に計算する
        if (cnt % 2 == 0) {
            p = DOUBLE(cnt / 2 + 1) / (cnt + 1);
        } else {
            p = 0.5;
        }
        ans += p * mul;

        mul = 1;
        // mulの初期化を忘れないように
    }

    fcout << ans << endl;
    return 0;
}